Sectriz de Maclaurin

Sectriz de Maclaurin: ejemplo con q0=PI/2 y K=3

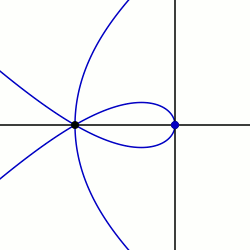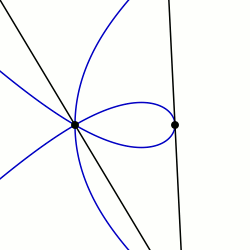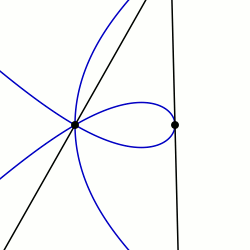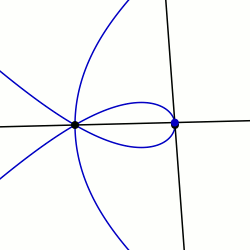
En geometría, una sectriz de Maclaurin se define como la curva barrida por el punto de intersección de dos líneas rectas que giran cada una a tasas constantes alrededor de diferentes puntos llamados polos. De manera equivalente, una sectriz de Maclaurin se puede definir como una curva cuya ecuación en coordenadas biangulares es lineal. El nombre se deriva de la trisectriz de Maclaurin (llamada así en referencia al matemático Colin Maclaurin), que es un miembro prominente de la familia de curvas, y su propiedad como sectriz, lo que significa que se puede usar para dividir un ángulo en un número determinado de partes iguales. Hay casos especiales que también se conocen como arácnidas o aracneidas debido a su forma similar a una araña, y curvas de Plateau en referencia al matemático que las estudió, Joseph-Antoine Ferdinand Plateau.

Ecuaciones en coordenadas polares

Sean dos líneas rectas que giran alrededor de dos polos $P$ y $P_1$. Por traslación y rotación se puede asumir que $P=(0,0)$ y que $P_1=(a,0)$. En el momento $t$, la recta que gira alrededor de $P$ tiene un ángulo $\theta =\kappa t+\alpha$ y la recta que gira alrededor de $P_1$ tiene un ángulo ${\theta }_1={\kappa }_{1}t+{\alpha }_1$, donde $\kappa$, $\alpha$, ${\kappa }_1$ y ${\alpha }_1$ son constantes. Eliminando $t$, se obtiene ${\theta }_1=q\theta +{\theta }_0$ donde $q={\kappa }_1/\kappa$ y ${\theta }_0={\alpha }_1-q\alpha$. Se supone que $q$ es racional; de lo contrario, la curva no es algebraica y es densa en el plano. Sea $Q$ el punto de intersección de las dos líneas y sea $\psi$ el ángulo en $Q$, entonces $\psi ={\theta }_1-\theta$. Si $r$ es la distancia de $P$ a $Q$ entonces, por el teorema de los senos,

$\frac{r}{\sin {\theta }_1}=\frac{a}{\sin \psi }$

así que

$r=a\frac{\sin {\theta }_1}{\sin \psi }=a\frac{\sin [q\theta +{\theta }_0]}{\sin [(q-1)\theta +{\theta }_0]}$

es la ecuación en coordenadas polares.

El caso con ${\theta }_0=0$ y $q=n$ donde $n$ es un número entero mayor que 2, se obtienen curvas arácnidas o aracneidas:

$r=a\frac{\sin n\theta }{\sin (n-1)\theta }$

El caso con ${\theta }_0=0$ y $q=-n$ donde $n$ es un número entero mayor que 1, se obtienen formas alternativas de curvas arácnidas o aracneidas:

$r=a\frac{\sin n\theta }{\sin (n+1)\theta }$

Con una operación similar a la anterior, resulta

$r_1=(-a)\frac{\sin [(1/q){\theta }_1-{\theta }_0/q]}{\sin [(1/q-1){\theta }_1-{\theta }_0/q]}$

como la ecuación polar (en $r_1$ y ${\theta }_1$) si el origen se desplaza a la derecha la distancia $a$. Téngase en cuenta que esta es la ecuación anterior con un cambio de parámetros, lo que es de esperar por el hecho de que dos polos son intercambiables en la construcción de la curva.

Ecuaciones en el plano complejo, coordenadas rectangulares y trayectorias ortogonales

Sea $q=m/n$ donde $m$ y $n$ son números enteros y la fracción es irreducible. En la notación de la sección anterior, se tiene que

${\theta }_1=q\theta +{\theta }_0$ o

$n{\theta }_1=m\theta +n{\theta }_0$.

Si $z=x+iy$ entonces $\theta =\arg (z),{\theta }_1=\arg (z-a)$, entonces la ecuación se convierte en

$n\arg (z-a)=m\arg (z)+n{\theta }_0$ o

$m\arg (z)-n\arg (z-a)=\arg (z^m(z-a{)}^{-n})=const$, que también se puede escribir como

$\frac{\mathrm{Re}(z^m(z-a{)}^{-n})}{\mathrm{Im}(z^m(z-a{)}^{-n})}=const.$

de donde es relativamente sencillo obtener la ecuación cartesiana dados m y n. La función

$w=z^m(z-a{)}^{-n}$ es analítica, por lo que las trayectorias ortogonales de la familia $arg(w)=const.$ son las curvas $|w|=const$

o también

$\frac{|z{|}^m}{|z-a{|}^n}=const.$

Ecuaciones paramétricas

Sea $q=m/n$ donde $m$ y $n$ son números enteros, y sea $\theta =np$ donde $p$ es un parámetro. Entonces, convertir la ecuación polar anterior a una ecuación paramétrica produce

$x=a\frac{\sin [mp+{\theta }_0]\cos np}{\sin [(m-n)p+{\theta }_0]},y=a\frac{\sin [mp+{\theta }_0]\sin np}{\sin [(m-n)p+{\theta }_0]}$.

La aplicación de la regla de la suma de ángulos para el seno produce

$x=a\frac{\sin [mp+{\theta }_0]\cos np}{\sin [(m-n)p+{\theta }_0]}=a+a\frac{\cos [mp+{\theta }_0]\sin np}{\sin [(m-n)p+{\theta }_0]}=\frac{a}{2}+\frac{a}{2}\frac{\sin [(m+n)p+{\theta }_0]}{\sin [(m-n)p+{\theta }_0]}$.

Entonces, si el origen se desplaza hacia la derecha por a/2, entonces las ecuaciones paramétricas son

$x=\frac{a}{2}\cdot \frac{\sin [(m+n)p+{\theta }_0]}{\sin [(m-n)p+{\theta }_0]},y=a\frac{\sin [mp+{\theta }_0]\sin np}{\sin [(m-n)p+{\theta }_0]}$.

Estas son las ecuaciones para las curvas de Plateau cuando ${\theta }_0=0$, o

$x=\frac{a}{2}\frac{\sin (m+n)p}{\sin (m-n)p},y=a\frac{\sin mp\sin np}{\sin (m-n)p}$.

Tripletes inversos

La curva inversa con respecto al círculo con radio a y centro en el origen de

$r=a\frac{\sin [q\theta +{\theta }_0]}{\sin [(q-1)\theta +{\theta }_0]}$

es

$r=a\frac{\sin [(q-1)\theta +{\theta }_0]}{\sin [q\theta +{\theta }_0]}=a\frac{\sin [(1-q)\theta -{\theta }_0]}{\sin [((1-q)-1)\theta -{\theta }_0]}$.

Esta es otra curva de la familia. La inversa con respecto al otro polo produce otra curva más de la misma familia y las dos inversas son a su vez inversas entre sí. Por lo tanto, cada curva de la familia es miembro de un triplete, de forma que cada una de las tres curvas pertenece a la familia y es inversa de las otras dos. Los valores de q en esta familia son

$q,\frac{1}{q},1-q,\frac{1}{1-q},\frac{q-1}{q},\frac{q}{q-1}$.

Propiedades de la sectriz

Sea $q=m/n$, donde $m$ y $n$ son números enteros que forman una fracción irreducible, y supóngase que ${\theta }_0$ es construible con regla y compás. El valor de ${\theta }_0$ suele ser 0 en la práctica, por lo que normalmente no es un problema. Sea $\phi$ un ángulo dado y supóngase que la sectriz de Maclaurin se ha dibujado con los polos $P$ y $P_1$ según la construcción anterior. Construir un radio desde $P_1$ según el ángulo $\phi +{\theta }_0$ y sea $Q$ el punto de intersección del radio y la sectriz, y dibujar $PQ$. Si $\theta$ es el ángulo de esta línea, entonces

$\phi +{\theta }_0={\theta }_1=q\theta +{\theta }_0$

así que $\theta =\frac{n\phi }{m}$. Restando repetidamente $\theta$ y $\phi$ entre sí como en el algoritmo de Euclides, se puede construir el ángulo $\phi /m$. Por lo tanto, la curva es una m-sectriz, lo que significa que con la ayuda de la curva se puede dividir un ángulo arbitrario por cualquier número entero. Esta es una generalización del concepto de trisectriz, del que se muestran ejemplos más adelante.

Ahora, dibujar un radio con ángulo $\phi$ desde $P$, y sea $Q^{\prime }$ el punto de intersección de este rayo con la curva. El ángulo de $P^{\prime }{Q}^{\prime }$ es

${\theta }_1=q\theta +{\theta }_0=q\phi +{\theta }_0$

y al restar ${\theta }_0$ se obtiene un ángulo de

$q\phi =\frac{m\phi }{n}$.

Al aplicar nuevamente el algoritmo de Euclides, se obtiene un ángulo de $\phi /n$ que muestra que la curva también es una n-sectriz.

Finalmente, dibujar un radio desde $P$ con ángulo $\pi /2-\phi -{\theta }_0$ y un radio desde $P^{\prime }$ con ángulo $\pi /2+\phi +{\theta }_0$, y sea $C$ el punto de intersección. Este punto está en la bisectriz perpendicular de $P{P}^{\prime }$, por lo que hay un círculo con centro $C$ que contiene a $P$ y a $P^{\prime }$. $\mathrm{\angle }PC{P}^{\prime }=2(\phi +{\theta }_0)$ por lo que cualquier punto del círculo forma un ángulo de $\phi +{\theta }_0$ entre $P$ y $P^{\prime }$. Esta es, de hecho, una de las circunferencias de Apolonio de P y P' .) Sea $Q^{″}$ el punto de intersección de esta circunferencia y la curva. Entonces

$\phi +{\theta }_0=\mathrm{\angle }P{Q}^{″}{P}^{\prime }=\psi ={\theta }_1-\theta =(q-1)\theta +{\theta }_0$

así que

$\phi =\frac{(m-n)\theta }{n},\theta =\frac{n\theta }{m-n}$.

Al aplicar el algoritmo de Euclides por tercera vez, se obtiene un ángulo de $\phi /(m-n)$, lo que muestra que la curva también es una (m-n)-sectriz.

Casos específicos

Cuatro casos de la sectriz de Maclaurin, para valores racionales de k=n/m que van de 1/5 a 4/5. Con k =4/5 la curva consta de cuatro bucles. Cuando el denominador n=1, entonces dos de los bucles se transforman en cuatro asíntotas

$q=0$

Esta es la curva

$r=a\frac{\sin {\theta }_0}{\sin (-\theta +{\theta }_0)}$

que es la línea recta a través de $(a,0)$

$q=1$

Este caso es una circunferencia que contiene el origen y $(a,0)$. Tiene ecuación polar

$r=a\frac{\sin (\theta +{\theta }_0)}{\sin {\theta }_0}$.

Es la curva inversa con respecto al origen del caso q=0. Las trayectorias ortogonales de la familia de círculos es la familia $\frac{|z-a|}{|z|}=const.$ Estas forman las circunferencias de Apolonio con polos $(0,0)$ y $(a,0)$.

$q=-1$

Estas curvas tienen ecuación polar

$r=a\frac{\sin (-\theta +{\theta }_0)}{\sin (-2\theta +{\theta }_0)}$,

ecuación compleja $arg(z(z-a))=const.$ En coordenadas rectangulares esto se convierte en $x^2-y^2-x=c(2xy-y)$ que es una cónica. De la ecuación polar es evidente que las curvas tienen asíntotas en $\theta ={\theta }_0/2$ y ${\theta }_0/2+\pi /2$ que son ángulos rectos. Entonces, las cónicas son, de hecho, hipérbolas equiláteras. El centro de la hipérbola es siempre $(a/2,0)$. Las trayectorias ortogonales de esta familia están dadas por $|z||z-a|=c$ que es la familia de óvalos de Cassini con focos $(0,0)$ y $(a,0)$.

Trisectriz de Maclaurin

En el caso que $q=3$ (o $q=1/3$ cambiando los polos) y ${\theta }_0=0$, la ecuación es

$r=a\frac{\sin 3\theta }{\sin 2\theta }=\frac{a}{2}\frac{4{\cos }^2\theta -1}{\cos \theta }=\frac{a}{2}(4\cos \theta -\sec \theta )$.

Esta curva es la trisectriz de Maclaurin que es un caso específico cuya generalización es la sectriz de Maclaurin. La construcción anterior proporciona un método por el que esta curva se puede utilizar como trisectriz.

Trisectriz caracol y rosa polar

En el caso que $q=3/2$ (o $q=2/3$ cambiando los polos) y ${\theta }_0=0$, la ecuación es

$r=a\frac{\sin \frac{3}{2}\theta }{\sin \frac{1}{2}\theta }=a(3{\cos }^2\frac{1}{2}\theta -{\sin }^2\frac{1}{2}\theta )=a(1+2\cos \theta )$.

Esta curva es la trisectriz caracol.

La ecuación que toma el origen como el otro polo es la curva denominada rosa polar, que tiene la misma forma.

$r=-a\frac{\sin \frac{2}{3}\theta }{\sin -\frac{1}{3}\theta }=2a\cos \frac{1}{3}\theta$.

El 3 en el numerador de q y la construcción anterior dan un método por el cual la curva puede usarse como trisectriz.

Bibliografía

• "Sectrice de Maclaurin" en Encyclopédie des Formes Mathématiques Remarquables (en francés)
• Plantilla:MathWorld
• Plantilla:MathWorld