Teorema de la velocidad media

La demostración de Galileo para el movimiento de los cuerpos en caída (s. XVII) fue idéntica la demostración geométrica del teorema del valor medio, hecha por Nicolás Oresme en el Plantilla:Siglo.

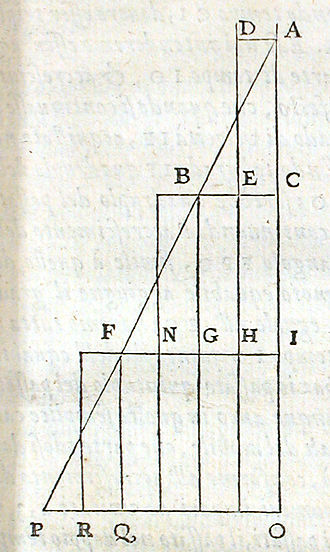
El Teorema de la velocidad media fue el teorema de mayor éxito intelectual de los denominados Calculatores de Merton College, de la Universidad de Oxford, en la primera mitad del Plantilla:Siglo. También estuvo muy presente en escritos de personalidades importantes de la Universidad de París, como Nicole d'Oresme.

Usando un lenguaje cinemático y simplificado, el teorema establece que un cuerpo en movimiento uniformemente acelerado recorre, en un determinado intervalo de tiempo, el mismo espacio que sería recorrido por un cuerpo que se desplazara con velocidad constante e igual a la velocidad media del primero.

Más tarde, este teorema compondría la base de la "ley de la caída de los cuerpos", de Galileo.

Hoy sabemos que las principales propiedades cinemáticas del movimiento rectilíneo uniformemente variado (MRUV), que aún se le atribuyen a Galileo por los textos de física, fueron descubiertas y probadas por los académicos del Plantilla:Siglo.

Demostración matemática

Sabemos que $$a=\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dv}{dx}$$En un movimiento uniformemente acelerado la aceleración es constante y por tanto:

- Integrando $dv=adt$ entre 0 y t obtenemos: $v_f-v_0=a\cdot t$

- Integrando $adx=vdv$ entre 0 y e y las velocidades inicial $v_0$ y final $v_f$ obtenemos:$$a\cdot e=\frac{1}{2}(v_f^2-v_0^2)=\frac{1}{2}(v_f-v_0)(v_f+v_0)$$

Sustituyendo la primera expresión en la segunda obtenemos:

$e=\frac{v_f+v_0}{2}t$

Véase también

• Ciencia medieval
• Universidad medieval