Fórmula de De Moivre

La fórmula de De Moivre, nombrada así por Abraham de Moivre afirma que para cualquier número complejo (y en particular, para cualquier número real) $x$ y para cualquier $n\in \mathbb{Z}$ se verifica que

$(\cos (x)+i\mathrm{sen}(x){)}^n=\cos (nx)+i\mathrm{sen}(nx)$.

Esta fórmula conecta los números complejos (i significa unidad imaginaria) con la trigonometría.

La expresión $\cos x+i\mathrm{sen}x$ en ocasiones se abrevia como $\mathrm{cis}x$.

Al expandir la parte izquierda de la igualdad y comparando la parte real con la imaginaria, es posible obtener expresiones muy útiles para $\cos (nx)$ y $\mathrm{sen}(nx)$ en términos de $\cos x$ y $\mathrm{sen}x$. Además, esta fórmula puede ser utilizada para encontrar expresiones explícitas para la $n$-ésima raíz de la unidad, eso es, números complejos $z$ tal que $z^n=1$.

Historia

Sello con la efigie de Euler

La forma actual de la fórmula aparece en la obra Introductio in analysin infinitorum de Euler, que la demuestra para todos los enteros naturales $n$ en 1748. Pero también aparece implícitamente en los trabajos de Abraham de Moivre varias veces desde 1707, en su trabajo sobre las raíces $n$-ésimas de números complejos. De hecho, los dos problemas están relacionados: escribir que Plantilla:Math es equivalente a decir que Plantilla:Math es una de las raíces enésimas del complejo Plantilla:Math.

Relación con la fórmula de Euler

La fórmula de Moivre puede ser obtenida de la fórmula de Euler:

$e^{ix}=\cos x+i\mathrm{sen}x$

aplicando leyes de la exponenciación

${\left(e^{ix}\right)}^n=e^{inx}$

Entonces, por la fórmula de Euler,

$e^{i(nx)}=\cos (nx)+i\mathrm{sen}(nx)$.

Algunos resultados

Partiendo nuevamente de la fórmula de Euler:

$e^{ix}=\cos x+i\mathrm{sen}x$

si hacemos $x=\pi$ entonces tenemos la identidad de Euler:

$\begin{array}{cc}{e}^{i\pi }& =\cos \pi +i\sin \pi \\ & =-1+0\\ & =-1\end{array}$

Es decir:

$e^{i\pi }=-1$

Además como tenemos estas dos igualdades:

$e^{ix}=\cos x+i\mathrm{sen}x$

$e^{-ix}=\cos x-i\mathrm{sen}x$

podemos deducir lo siguiente:

$\begin{array}{cc}\cos x& =\frac{e^{ix}+e^{-ix}}{2}\\ \mathrm{sen}x& =\frac{e^{ix}-e^{-ix}}{2i}\end{array}$

Demostración por inducción

Consideramos tres casos.

Para un entero $n>0$, procedemos por inducción matemática. Cuando $n=1$ el resultado es claramente cierto. Para nuestra hipótesis asumimos que el resultado es verdadero para algún entero positivo $k$. Eso es que asumimos:

${(\cos x+i\mathrm{sen}x)}^k=\cos (kx)+i\mathrm{sen}(kx)$

Ahora, considerando el caso $n=k+1$:

$\begin{array}{cc}{(\cos x+i\mathrm{sen}x)}^{k+1}& ={(\cos x+i\mathrm{sen}x)}^k(\cos x+i\mathrm{sen}x)\\ & =[\cos \left(kx\right)+i\mathrm{sen}\left(kx\right)](\cos x+i\mathrm{sen}x)\text{por la hipótesis de inducción}\\ & =\cos \left(kx\right)\cos x-\mathrm{sen}\left(kx\right)\mathrm{sen}x+i[\cos \left(kx\right)\mathrm{sen}x+\mathrm{sen}\left(kx\right)\cos x]\\ & =\cos \left[(k+1)x\right]+i\mathrm{sen}\left[(k+1)x\right]\text{por las identidades trigonométricas}\end{array}$

Deducimos que el resultado es verdadero para n = k + 1 cuando es verdadero para n = k. Por el principio de la inducción matemática se desprende que el resultado es verdadero para todos los enteros positivos n≥1.

Cuando $n=0$ la fórmula es verdadera ya que $\cos (0x)+i\mathrm{sen}(0x)=1+i0=1$, y (por convención) $z^0=1$.

Cuando $n<0$, consideramos que existe un entero positivo $m$ tal que $n=-m$, por lo que

$\begin{array}{cc}{(\cos x+i\mathrm{sen}x)}^n& ={(\cos x+i\mathrm{sen}x)}^{-m}\\ & =\frac{1}{{(\cos x+i\mathrm{sen}x)}^m}\\ & =\frac{1}{(\cos mx+i\mathrm{sen}mx)}\\ & =\cos \left(mx\right)-i\mathrm{sen}\left(mx\right)\\ & =\cos (-mx)+i\mathrm{sen}(-mx)\\ & =\cos \left(nx\right)+i\mathrm{sen}\left(nx\right).\end{array}$

Por lo tanto el teorema es verdadero para todo $n\in \mathbb{Z}$.

Generalización

La fórmula en realidad es verdadera en un campo mucho más general que el presentado arriba: si z y w son números complejos, entonces

${(\cos z+i\mathrm{sen}z)}^w$

es una función multivaluada mientras

$\cos (wz)+i\mathrm{sen}(wz)$

no lo sea. Por lo tanto se puede asegurar que:

$\cos (wz)+i\mathrm{sen}(wz)$     es un valor de     ${(\cos z+i\sin z)}^w$.

Aplicaciones

Raíces cúbicas de la unidad.

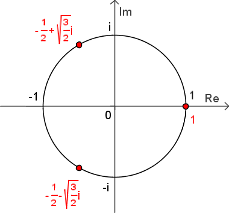
Esta fórmula puede ser utilizada para encontrar tanto la potencia como las raíces enésimas de un número complejo escrito en la forma polar.

$z=r(\cos x+i\mathrm{sen}x)$

Si el número complejo está en forma binómica, primero hay que convertirlo a forma polar, siendo $r$ el módulo.

Potencia

Para obtener la potencia del número complejo se aplica la fórmula:

$z^n={[|z|(\cos (x)+i\mathrm{sen}(x))]}^n=|z{|}^n[\cos (nx)+i\mathrm{sen}(nx)]$

Raíces

Para obtener las $n$ raíces de un número complejo, se aplica:

$z^{1/n}={\left[r(\cos x+i\mathrm{sen}x)\right]}^{1/n}=r^{1/n}[\cos \left(\frac{x+2k\pi }{n}\right)+i\mathrm{sen}\left(\frac{x+2k\pi }{n}\right)]$

donde $k$ es un número entero que va desde $0$ hasta $n-1$, que al sustituirlo en la fórmula permite obtener las $n$ raíces diferentes de $z$.

Véase también

• Fórmula de Euler
• Raíz de la unidad
• Números imaginarios

Enlaces externos

• Plantilla:Springer
• De Moivre's Theorem for Trig Identities by Michael Croucher, Wolfram Demonstrations Project.

Plantilla:Control de autoridades