Archivo:Ehrenfest-paradox-disk.svg
Ir a la navegación
Ir a la búsqueda
Tamaño de esta previsualización PNG del archivo SVG: 220 × 180 píxeles. Otras resoluciones: 293 × 240 píxeles | 587 × 480 píxeles | 939 × 768 píxeles | 1252 × 1024 píxeles | 2503 × 2048 píxeles.
Archivo original (archivo SVG, nominalmente 220 × 180 píxeles, tamaño de archivo: 4 kB)
Resumen
| Descripción |
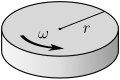
English: The Ehrenfest paradox in special relativity describes a spinning cylinder, which should contract around the circumference due to Lorentz-contraction, while its radius remains constant. The graphic shows rulers which rest in the laboratory system and rulers attached to the cylinder, which get contracted relatively to the laboratory system.
Deutsch: Das Ehrenfestsche Paradoxon der Speziellen Relativitätstheorie beschreibt einen rotierenden Zylinder, der sich entlang seinem Umfang aufgrund der Lorentzkontraktion kontrahieren sollte, während sein Radius konstant bleibt. Die Grafik zeigt Maßstäbe die im Laborsystem ruhen, so wie Maßstäbe die mit dem Zylinder rotieren und deshalb relativ zum Laborsystem kontrahiert werden. |
| Fecha | |
| Fuente | Trabajo propio |
| Autor | Geek3 |
| Otras versiones |
|
Source code
The image is created by the following source-code. Requirements:
python source code:
#!/usr/bin/python
# -*- coding: utf8 -*-
try:
import svgwrite as svg
except ImportError:
print 'You need to install svgwrite: http://pypi.python.org/pypi/svgwrite/'
exit(1)
from math import *
size = 220, 180
rx, ry = size[0] / 2 - 3, 50
v = float(ry) / float(rx)
l = 40
lw = 2
# document
doc = svg.Drawing('ehrenfest-paradox-disk.svg', size=size)
doc['stroke-width'] = lw
doc['fill'] = 'white'
doc['stroke'] = 'black'
doc['stroke-linejoin'] = 'miter'
# background
doc.add(doc.rect(id='background', insert=(0, 0), size=size, stroke='none'))
# disk
grad = doc.defs.add(doc.linearGradient(id='grad', start=('0%',0), end=('100%',0), gradientUnits='objectBoundingBox'))
grad.add_stop_color(offset=0, color='#F7F7F7')
grad.add_stop_color(offset=0.5, color='#DDD')
grad.add_stop_color(offset=1, color='#999')
disk = doc.add(doc.g(id='disk', transform='translate(' + str(size[0]/2) + ',' + str(ry+3) + ')'))
path = 'M ' + str(-rx) + ',0 V ' + str(l)
path += ' A ' + str(rx) + ',' + str(ry) + ' 0 1 0 ' + str(rx) + ',' + str(l)
path += ' V 0 Z'
disk.add(doc.path(d=path, fill='url(#grad)', stroke_linejoin='bevel'))
disk.add(doc.ellipse(center=(0, 0), r=(rx, ry), fill='#D8D8D8'))
disk.add(doc.ellipse(center=(0, 0), r=(2, 2.0*v), fill='black'))
radius_angle = radians(-40.0)
csr = cos(radius_angle), sin(radius_angle)
disk.add(doc.line(start=(0,0), end=(rx*csr[0], ry*csr[1]),
stroke_width=lw*sqrt(csr[0]**2 + (v*csr[1])**2)))
# round arrow
ar, aw, ah, ab, al, a0, a1 = 0.7*rx, 7, 2, 1, 3, radians(160), radians(100)
apath = 'M ' + str(ar*cos(a0)) + ',' + str(ar*sin(a0))
apath += ' A %f,%f 0 0 0 %f,%f' % (ar, ar, ar*cos(a1), ar*sin(a1))
arrowhead = doc.defs.add(doc.marker(id='arrowhead', orient='auto', overflow='visible'))
arrowhead.add(doc.path(fill='black', stroke='none',
d='M 0.0,0.0 L %f,%f L %f,0 L %f,%f L 0,0 z'%(-ab, -ah, al, -ab, ah)))
arrow = doc.path(d=apath, fill='none', stroke_width=aw, transform='scale(1,' + str(v) + ')')
arrow['marker-end'] = arrowhead.get_funciri()
disk.add(arrow)
# ruler
ruler = doc.defs.add(doc.g(id='ruler'))
rw, rh, rn = 32, 14, 4
ruler.add(doc.path(d='M 0,0 H %f V %f H 0 V 0 Z'%(rw+3, rh),
fill='white', stroke='none'))
squares = ''
for i in range(rn/2):
squares += 'M %f,0 H %f V %f H %f V 0 Z '%(i*rw*2./rn, (1+i*2.)*rw/rn, rh, i*rw*2./rn)
ruler.add(doc.path(d=squares, fill='red', stroke='none'))
ruleredge = 'M %f,0 H %f V %f H 0 V 0 H %f V %f'%(rw, 3+rw, rh, rw, rh)
for i in range(1, rn):
ruleredge += ' M %f,0 V %f'%(i*rw/float(rn), rh/2.)
ruler.add(doc.path(d=ruleredge, fill='none', stroke='black', stroke_width=lw, stroke_linecap='round'))
rulers = doc.add(doc.g(id='rulers'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.89, 0.42, 0, 1, 17, 134)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(1.00, 0.16, 0, 1, 54, 150)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(1.00, 0.00, 0, 1, 95, 156)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.53, 0.33, 0, 1, 16.53, 91)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.57, 0.19, 0, 1, 39, 104)'))
rulers.add(doc.use(ruler, insert=(0, 0), transform='matrix(0.60, 0.10, 0, 1, 63, 112)'))
doc.add(doc.path(d='M 16.5,106 V 133', fill='none', stroke_width=1, stroke_dasharray='4,2'))
doc.add(doc.path(d='M 84.5,130 V 154', fill='none', stroke_width=1, stroke_dasharray='4,2'))
# text
doc.add(doc.path(id='omega', stroke='none', fill='black',
transform='translate(70,70) scale(0.03,-0.03)',
d='M 13 0 m 251 82 c 9 -63 43 -93 94 -93 c 59 0 113 38 153 93 c 75 104 94 \
255 94 289 c 0 71 -37 71 -43 71 c -25 0 -50 -26 -50 -48 c 0 -13 6 -19 15 -27 \
c 32 -33 35 -65 35 -87 c 0 -85 -85 -219 -190 -219 c -9 0 -37 0 -55 23 c -12 \
16 -20 35 -20 55 c 0 3 0 5 6 16 c 19 45 33 100 33 113 c 0 12 -7 23 -21 23 c \
-11 0 -20 -9 -28 -25 c -2 -5 -14 -49 -21 -101 c -2 -18 -2 -20 -9 -27 c -44 \
-61 -90 -77 -124 -77 c -66 0 -88 55 -88 114 c 0 75 37 158 84 225 c 10 14 10 \
16 10 19 c 0 8 -6 12 -12 12 c -16 0 -62 -88 -76 -120 c -37 -89 -38 -171 -38 \
-180 c 0 -80 30 -142 106 -142 c 65 0 113 46 145 93 z'))
doc.add(doc.path(id='r', stroke='none', fill='black',
transform='translate(152,60) scale(0.03,-0.03)',
d='M 29 0 m 59 59 c -3 -15 -9 -38 -9 -43 c 0 -18 14 -27 29 -27 c 12 0 30 8 \
37 28 c 2 4 36 140 40 158 c 8 33 26 103 32 130 c 4 13 32 60 56 82 c 8 7 37 33 \
80 33 c 26 0 41 -12 42 -12 c -30 -5 -52 -29 -52 -55 c 0 -16 11 -35 38 -35 c \
27 0 55 23 55 59 c 0 35 -32 65 -83 65 c -65 0 -109 -49 -128 -77 c -8 45 -44 \
77 -91 77 c -46 0 -65 -39 -74 -57 c -18 -34 -31 -94 -31 -97 c 0 -10 10 -10 12 \
-10 c 10 0 11 1 17 23 c 17 71 37 119 73 119 c 17 0 31 -8 31 -46 c 0 -21 -3 \
-32 -16 -84 z'))
doc.save()
Licencia
Yo, titular de los derechos de autor de esta obra, la publico en los términos de las siguientes licencias:
|
Se autoriza la copia, distribución y modificación de este documento bajo los términos de la licencia de documentación libre GNU, versión 1.2 o cualquier otra que posteriormente publique la Fundación para el Software Libre; sin secciones invariables, textos de portada, ni textos de contraportada. Se incluye una copia de la dicha licencia en la sección titulada Licencia de Documentación Libre GNU. |
Este archivo se encuentra bajo la licencia Atribución 3.0 No portada de Creative Commons.
- Eres libre:
- de compartir – de copiar, distribuir y transmitir el trabajo
- de remezclar – de adaptar el trabajo
- Bajo las siguientes condiciones:
- atribución – Debes otorgar el crédito correspondiente, proporcionar un enlace a la licencia e indicar si realizaste algún cambio. Puedes hacerlo de cualquier manera razonable pero no de manera que sugiera que el licenciante te respalda a ti o al uso que hagas del trabajo.
Puedes usar la licencia que prefieras.
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 01:35 21 ene 2013 | | 220 × 180 (4 kB) | wikimediacommons>Geek3 | {{Information |Description ={{en|1=Ehrenfest paradox illustration}} |Source ={{own}} |Author =Geek3 |Date ={{Date|2013|01|21}} |Permission = |other_versions = }} |
Usos del archivo
La siguiente página usa este archivo:
