Archivo:Steiner chain animation-50dpi.gif
De testwiki
Ir a la navegación
Ir a la búsqueda
Steiner_chain_animation-50dpi.gif (250 × 251 píxeles; tamaño de archivo: 1,35 MB; tipo MIME: image/gif, bucleado, 126 frames)
Este archivo es de Wikimedia Commons y puede usarse en otros proyectos. La descripción en su página de descripción del archivo se muestra debajo.
Resumen
| DescripciónSteiner chain animation-50dpi.gif |
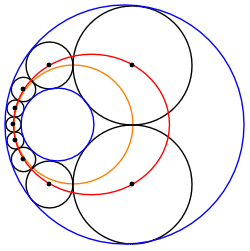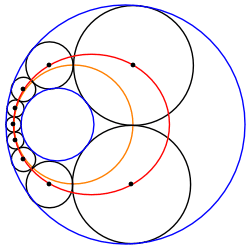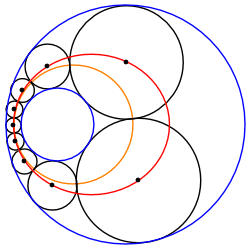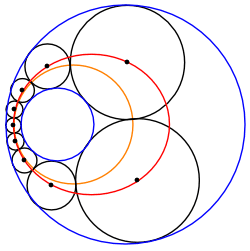
English: Animation of a Steiner chain of 9 circles, showing that the locus of the position of the circles' centres is an ellipse (in red), and that the locus of the contact points between the circles is a circle itself (in orange) |
| Fecha | |
| Fuente | https://twitter.com/j_bertolotti/status/1039543306433249280 |
| Autor | Jacopo Bertolotti |
| Permiso (Reutilización de este archivo) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 11.0 code
n = 9;
\[Theta] = \[Pi]/n;
\[CapitalDelta]\[Theta] = (2 \[Pi])/n;
R = 0.2;
\[Rho] = R/(1 + 1/Sin[\[Theta]]);
r = \[Rho] (1/Sin[\[Theta]] - 1);
center = {.3, 0};
plots = Reap[For[start = 0, start <= 2 \[Pi], start = start + 0.05,
CandR =
Table[{center[[1]] + (\[Rho] + r) Cos[i],
center[[2]] + (\[Rho] + r) Sin[i], \[Rho]}, {i, start,
start + (n -
1)*\[CapitalDelta]\[Theta], \[CapitalDelta]\[Theta]}];
createcoord[{x_, y_,
z_}] := {(x )/(x^2 + y^2 - z^2), (y)/(x^2 + y^2 - z^2),
z/(x^2 + y^2 - z^2)};
innerc = createcoord[Flatten[{center, r}]];
outherc = createcoord[Flatten[{center, R}]];
ellipseCenter = {(outherc[[1]] + innerc[[1]])/2, 0};
ellipseA =
Abs[createcoord[{center[[1]] + \[Rho] + r, 0, \[Rho]}][[1]] -
ellipseCenter[[1]]];
ellipseC = (outherc[[1]] - innerc[[1]])/2;
ellipseB = Sqrt[ellipseA^2 - ellipseC^2];
tmp = Map[createcoord, CandR];
p1 = {x, y} /.
Solve[{(x - tmp[[1, 1]])^2 + (y - tmp[[1, 2]])^2 ==
tmp[[1,
3]]^2 && (x - tmp[[2, 1]])^2 + (y - tmp[[2, 2]])^2 ==
tmp[[2, 3]]^2}, {x, y}][[1]];
p2 = {x, y} /.
Solve[{(x - tmp[[3, 1]])^2 + (y - tmp[[3, 2]])^2 ==
tmp[[3,
3]]^2 && (x - tmp[[2, 1]])^2 + (y - tmp[[2, 2]])^2 ==
tmp[[2, 3]]^2}, {x, y}][[1]];
p3 = {x, y} /.
Solve[{(x - tmp[[3, 1]])^2 + (y - tmp[[3, 2]])^2 ==
tmp[[3,
3]]^2 && (x - tmp[[4, 1]])^2 + (y - tmp[[4, 2]])^2 ==
tmp[[4, 3]]^2}, {x, y}][[1]];
c =
Abs[{xc, yc, rc} /.
Solve[((#1 - xc)^2 + (#2 - yc)^2 == rc^2) & @@@ {p1, p2,
p3}, {xc, yc, rc}][[1]] ];
Sow@Show[
Graphics[{Orange, Thick,
Evaluate[Circle[{c[[1]], c[[2]]}, c[[3]]] ]}],
Graphics[{Black, Thick,
Circle[{#1, #2}, #3] & @@@ Map[createcoord, CandR] }],
Graphics[{Blue, Thick,
Circle[{#1, #2}, #3] & @@@ {innerc, outherc} }],
Graphics[{Red, Thick,
Circle[ellipseCenter, {ellipseA, ellipseB}]}],
Graphics[{PointSize[0.02],
Point[Map[createcoord, CandR][[All, 1 ;; 2]]] }]
];
];][[2, 1]];
ListAnimate[plots]
Licencia
Yo, el titular de los derechos de autor de esta obra, la publico en los términos de la siguiente licencia:
| Este archivo está disponible bajo la licencia Dedicación de Dominio Público CC0 1.0 Dedicación a Dominio Público Universal de Creative Commons. | |
| La persona que ha asociado una obra a este documento lo dedica al dominio público mediante la cesión mundial de sus derechos bajo la ley de derechos de autor y todos los derechos legales adyacentes propios de dicha, en el ámbito permitido por ley. Puedes copiar, modificar, distribuir y reproducir el trabajo, incluso con objetivos comerciales, sin pedir aprobación del autor.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Este archivo, el cual fue publicado originalmente en https://twitter.com/j_bertolotti/status/1039543306433249280, fue revisado el 19 October 2018 por el revisor Ronhjones, quien confirmó que en esa fecha estaba disponible bajo la licencia indicada.
|
Leyendas
Añade una explicación corta acerca de lo que representa este archivo
Elementos representados en este archivo
representa a
Algún valor sin elemento de Wikidata
11 sep 2018
image/gif
1 410 765 byte
251 píxel
250 píxel
09fe40aeaa7cd25b2577f441581d8527522e4761
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 09:29 12 sep 2018 | 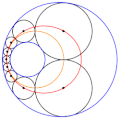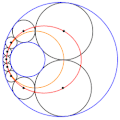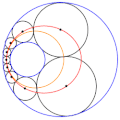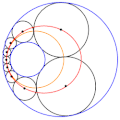 | 250 × 251 (1,35 MB) | wikimediacommons>Berto | User created page with UploadWizard |
Usos del archivo
La siguiente página usa este archivo: