Método de bisección

Unas cuantas iteraciones del método de bisección aplicadas en un intervalo [a₁;b₁]. El punto rojo es la raíz de la función.

En matemáticas, el método de bisección , también llamado dicotomía, es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz.

Introducción

Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones de una variable, también conocido como Método de Intervalo Medio. Se basa en el teorema del valor intermedio (TVI), el cual establece que toda función continua $f$ en un intervalo cerrado $[a,b]$ toma todos los valores que se hallan entre $f(a)$ y $f(b)$. Esto es que todo valor entre $f(a)$ y $f(b)$ es la imagen de al menos un valor en el intervalo $[a,b]$. En caso de que $f(a)$ y $f(b)$ tengan signos opuestos, el valor cero sería un valor intermedio entre $f(a)$ y $f(b)$, por lo que con certeza existe un $p\in [a,b]$ que cumple $f(p)=0$. De esta forma, se asegura la existencia de al menos una solución de la ecuación $f(x)=0$.

El método consiste en lo siguiente:

• Debe existir seguridad sobre la continuidad de la función $f$ en el intervalo $[a,b]$
• A continuación se verifica que $f(a)\cdot f(b)<0$
• Se calcula el punto medio $m$ del intervalo $[a,b]$ y se evalúa $f(m)$ si ese valor es igual a cero, ya hemos encontrado la raíz buscada
• En caso de que no lo sea, verificamos si $f(m)$ tiene signo opuesto con $f(a)$ o con $f(b)$
• Se redefine el intervalo $[a,b]$ como $[a,m]$ o $[m,b]$ según se haya determinado en cuál de estos intervalos ocurre un cambio de signo
• Con este nuevo intervalo se continúa sucesivamente encerrando la solución en un intervalo cada vez más pequeño, hasta alcanzar la precisión deseada

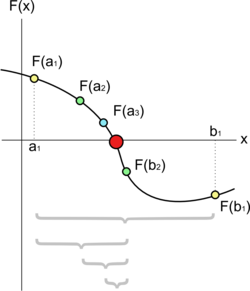
En la siguiente figura se ilustra el procedimiento descrito.

El método de bisección es menos eficiente que el método de Newton, pero es mucho más seguro para garantizar la convergencia. Si $f$ es una función continua en el intervalo $[a,b]$ y $f(a)f(b)<0$, entonces este método converge a la raíz de $f$. De hecho, una cota del error absoluto es: Plantilla:Ecuación en la n-ésima iteración. La bisección converge linealmente, por lo cual es un poco lento. Sin embargo, se garantiza la convergencia si $f(a)$ y $f(b)$ tienen distinto signo.

Si existieran más de una raíz en el intervalo entonces el método sigue siendo convergente pero no resulta tan fácil caracterizar hacia qué raíz converge el método.

Algoritmo

Para aplicar el método consideremos tres sucesiones $a_n\le r_n\le b_n$ definidas por las siguientes relaciones: Plantilla:Ecuación Donde los valores iniciales vienen dados por: Plantilla:Ecuación Se puede probar que las tres sucesiones convergen al valor de la única raíz del intervalo: Plantilla:Ecuación

Implementación en Python

from typing import Callable, Tuple

def bisection(f: Callable, a: float, b: float, xtol=0.001, maxiter=100) -> Tuple[float, int]:
    """
    Encuentra una raíz de la función f en el intervalo [a, b] utilizando el método de la bisección.

    :param f: La función cuya raíz se busca.
    :param a: Extremo izquierdo del intervalo.
    :param b: Extremo derecho del intervalo.
    :param xtol: Tolerancia de error en la raíz (diferencia mínima entre a y b).
    :param maxiter: Número máximo de iteraciones permitidas.
    :return: Una tupla que contiene la aproximación de la raíz y el número de iteraciones realizadas.
    :raise ValueError: Si f(a) y f(b) tienen el mismo signo, lo que significa que no hay una raíz en el intervalo.
    :raise Exception: Si se excede el número máximo de iteraciones permitidas.
    """

    if f(b) * f(a) > 0:
        raise ValueError('No existe raíz en el intervalo dado')

    nit = 0
    while nit <= maxiter:
        nit += 1
        c = (a + b) / 2
        if abs(f(c)) <= xtol:
            return c, nit
        elif f(c) * f(a) < 0:
            b = c
        else:
            a = c

    raise Exception("El número máximo de iteraciones permitidas ha sido excedido.")

Demostración de la convergencia

Suponiendo que se cumplen las condiciones iniciales para la puesta en práctica del algoritmo, definimos r como una raíz dentro del intervalo [a, b]. El intervalo de búsqueda en el n-ésimo paso tiene longitud:

Como $r_n$, que es la raíz n-ésima calculada, se encuentra siempre dentro del intervalo de búsqueda, tenemos entonces que:

Tomando límites,

Queda demostrado entonces, que si se cumplen las condiciones iniciales del problema, el método de bisección converge al menos, a una de las raíces que se encuentran en el intervalo señalado.

Cota de error

El error cometido tras realizar $n\ge 1$ iteraciones del método de bisección es

Para lograr un error inferior a $\epsilon$, el número de iteraciones $n$ a realizar debe ser

Bibliografía

• Richard L Burden, J. Douglas Faires (2000), "Numerical Analysis, (7th Ed)", Brooks/Cole. ISBN 0-534-38216-9.
• Plantilla:Citation