Topología cociente

Ilustración de un espacio cociente, S², obtenida por pegado del contorno (en azul) del disco D² a un solo punto.

En matemáticas, la topología cociente consiste intuitivamente en crear una topología pegando ciertos puntos sobre otros, en un espacio dado, por medio de una relación de equivalencia bien definida. El nuevo espacio así generado recibe el nombre de espacio cociente. Ejemplos conocidos son el toro matemático o la banda de Möbius.

Definición

Sean $(X,{𝒯}_X)$ un espacio topológico y $\sim$ una relación de equivalencia sobre $X$. El conjunto cociente $Y=X/\sim$ es el conjunto de clases de equivalencia de los elementos de $X$:

$Y=\{[x]:x\in X\}.$

Los conjuntos abiertos que conforman la llamada topología cociente sobre $Y$ son los conjuntos de las clases de equivalencia cuyas uniones son conjuntos abiertos en $X$:

${𝒯}_{\sim }=\{U\subseteq Y:\bigcup _{[x]\in U}[x]\in {𝒯}_X\}.$

Definición equivalente: sea la aplicación proyección $p:X\to X/\sim$ dada por $p(x)=[x]$, se definen los abiertos de ${𝒯}_{\sim }$ como los conjuntos $U\subseteq X/\sim$ tales que $p^{-1}(U)\subseteq X$ es abierto. Es decir, un conjunto de clases de equivalencia es abierto si los elementos que las forman son un conjunto abierto de la topología original.

Propiedades

• La aplicación proyección al cociente $p:X\to X/\sim$ que envía a cada elemento a su clase de equivalencia correspondiente es continuay la topología cociente es la más fina que se puede definir en $X/\sim$ que cumple esto. Es decir, la topología cociente es la topología final respecto a la proyección al cociente.Plantilla:Demostración
• Sean $p:X\to X/\sim$ la proyección al cociente y $f:X/\sim \to Y$ una aplicación. Entonces, la aplicación $f$ es continua si, y sólo si, la composición $f\circ p:X\stackrel{p}{\to }X/\sim \stackrel{f}{\to }Y$ es continua.Plantilla:Demostración
• La propiedad universal: La topología cociente es la única topología que cumple que para cualquier espacio topológico (Z, T) y cualquier función g:(Y, $T_f$) $\to$ (Z, T) se tiene que g es continua si y sólo si $g\circ f$ es continua

Ejemplos

En los siguientes ejemplos los homeomorfismos se construyen primero deformando el espacio cociente sin tener en cuenta la relación de equivalencia (cortándola) y después pegando los trozos que estaban relacionados. Es decir, estamos admitiendo que podemos construir un homeomorfismo entre dos espacios cociente a partir de uno entre los espacios originales siempre y cuando los elementos relacionados antes y después del homeomorfismo sean los mismos. Este resultado, que justifica que las construcciones siguientes son correctas, se conoce como lema de cortar y pegar, y se demuestra a continuación Plantilla:Demostración

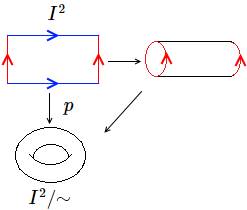
• El toro como conjunto cociente: Sobre $I^2=[0,1]\times [0,1]$ se define la relación de equivalencia $(x,0)\sim (x,1)$ y $(0,y)\sim (1,y)\mathrm{\forall }x,y\in [0,1]$. El espacio cociente $I^2/\sim$ es homeomorfo a un toro.

Toro

• La banda de Möbius como conjunto cociente: Sobre $I^2$ se define la relación de equivalencia $(0,y)\sim (1,1-y)\mathrm{\forall }y\in [0,1]$. El espacio cociente $I^2/\sim$ es homeomorfo a una banda de Möbius.

Banda de Möbius

• La botella de Klein como conjunto cociente: Sobre $I^2$ se define la relación de equivalencia $(x,0)\sim (x,1)$ y $(0,y)\sim (1,1-y)\mathrm{\forall }x,y\in [0,1]$. El espacio cociente $I^2/\sim$ es homeomorfo a una botella de Klein (es difícil de visualizar puesto que no es homeomorfo a un subespacio de ${ℝ}^3$).

• 
• 
• 
• 
• 
• 
• 

• La esfera como conjunto cociente: Sobre $\{(x,y):|x|+|y|\le 1\}$ (cuadrado de vértices $(1,0),(0,1),(-1,0),(0,-1)$) se define la relación de equivalencia $(x,y)\sim (-x,y)$ para $(x,y)$ de la frontera. El espacio cociente correspondiente es homeomorfo a una esfera.

Bibliografía

• Robles Corbalá Carlos Alberto, "Topología general" primera edición Universidad de Sonora.
• Plantilla:MathWorld
• Plantilla:PlanetMath
• Plantilla:Springer

Enlaces externos

• Plantilla:Cita web

Plantilla:Wikilibros incluyendo un capítulo sobre espacios cocientes.