Producto (teoría de categorías)

En teoría de categorías, el producto de dos (o más) objetos es una noción que captura la esencia detrás de otras construcciones en otras áreas de las matemáticas tales como producto cartesiano de conjuntos, el producto directo de grupos, producto directo de anillos, el producto de espacios topológicos entre otros. Esencialmente el producto de una familia de objetos es el "más general" de los objetos que admite morfismos a cada uno de los objetos dados.

Definición

Sea $C$ una categoría, $X_1$ y $X_2$ objetos de $C$. Un objeto $X$ es el producto de $X_1$ y $X_2$, denotado $X_1\times X_2$ si y solo si satisface la siguiente propiedad universal

Existe morfismos ${\pi }_1:X\to X_1,{\pi }_2:X\to X_2$, llamadas proyecciones canónicas o proyecciones tal que para cualquier otro objeto $Y$ y un par de morfismos $f_1:Y\to X_1,f_2:Y\to X_2$ existe un único morfismo $f:Y\to X$ tal que el siguiente diagrama conmuta:

Universal product of the product

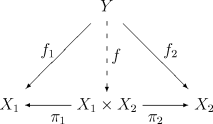
El único morfismo $f$ recibe el nombre de morfismo producto de $f_1$ y $f_2$ y se denota por $⟨f_1,f_2⟩$.

Se acaba de definir el producto binario. En lugar de dos objetos considere una familia arbitraria de objetos indicada por algún conjunto $I$. Entonces obtenemos la definición de un producto.

Un objeto $X$ es el producto de una familia $\{X_i{\}}_{i\in I}$ de objetos si y solo si existen morfismos ${\pi }_i:X\to X_i$, tal que para cualquier otro objeto $Y$ y una familia de morfismos $f_i:Y\to X_i$ indizados por $I$ existe un único morfismo $f:Y\to X$ tal que el siguiente diagrama conmuta para cualquier $i\in I$

Universal product of the product

El producto se denota como $\prod _{i\in I}{X}_i$; si $I=\{1,\dots ,n\}$, entonces se denota como $X_1\times \cdots \times X_n$ y el morfismo producto como $⟨f_1,\dots ,f_n⟩$.

De forma alterna, el producto puede ser definido totalmente mediante ecuaciones, aquí esta un ejemplo para el producto binario:

• La existencia de $f$ se garantizada por la operación $⟨-,-⟩$.
• La conmutatividad de los respectivos diagramas está garantizada por la igualdad $\mathrm{\forall }{f}_1,\mathrm{\forall }{f}_2,\mathrm{\forall }i\in \{1,2\},{\pi }_i\circ ⟨f_1,f_2⟩=f_i$.
• La Unicidad de $f$ es garantizada por la igualdad $\mathrm{\forall }f,⟨{\pi }_1\circ f,{\pi }_2\circ f⟩=f$.

También el producto puede ser obtenido a partir del límite. Una familia de objetos es un diagrama sin morfismos. Si consideramos nuestro diagrama como un funtor, entonces es un funtor desde $I$ considerada como una categoría discreta. Entonces la definición de producto coincide con la definición de cono límite para este funtor.

Ejemplos

En la categoría Set (la categoría de conjuntos) el producto para la categoría es el producto cartesiano. Dada una familia de conjuntos X_i el producto es definido como

$\prod _{i\in I}{X}_i:=\{(x_i{)}_{i\in I}|x_i\in X_i\mathrm{\forall }i\in I\}$

con las proyecciones

${\pi }_j:\prod _{i\in I}{X}_i\to X_j,{\pi }_j((x_i{)}_{i\in I}):=x_j$

Dado cualquier otro conjunto Y con una familia de funciones :$f_i:Y\to X_i$ la flecha universal f se define como

$f:Y\to \prod _{i\in I}{X}_i,f(y):=(f_i(y){)}_{i\in I}$

• En la categoría de espacios topológicos el producto categórico es el espacio topológico cuyo conjunto subyacente es el producto cartesiano con la topología producto.

• En la categoría de módulos sobre algún anillo R, el producto categórico está dado por el producto directo de módulos.

• En la categoría de grupos el producto categórico está dado por el producto cartesiano con la multiplicación definida componente a componente.

• En la categoría de variedades algebraicas el producto está dado por el encaje de Segre

• Un conjunto parcialmente ordenado puede ser considerado como una categoría, usando la relación de orden como los morfismos. En este caso los productos y coproductos son los ínfimos y supremos del conjunto respectivamente

• Un producto vacío (i.e. $I$ es el conjunto vacío) es un objeto terminal o final)

Discusión

El producto no necesariamente existe; por ejemplo considere una familia infinita de espacios métricos como ${ℝ}^{\mathbb{N}}$ y ${ℝ}^{ℝ}$, no existe tal cosa como el producto métrico de ellos.

Una categoría en donde para cualquier conjunto finito de objetos existe su producto entonces es llamada categoría cartesiana

Supongamos que $C$ es una categoría cartesiana y $1$ denota el objeto final de la categoría $C$. Entonces tenemos los siguientes isomorfismos naturales.

$X\times (Y\times Z)\simeq (X\times Y)\times Z$

$X\times 1\simeq 1\times X\simeq X$

$X\times Y\simeq Y\times X$

Estas propiedades son similares a aquellas dadas en un monoide conmutativo; una categoría que tiene productos finitos forma una categoría simétrica monoidal

Distributividad

En una categoría con productos y coproductos finitos existe un morfismo canónico X×Y+X×Z → X×(Y+Z), donde el signo aditivo denota el coproducto, para comprender esto observe que tenemos varias proyecciones e inyecciones canónicas que completan el diagrama:

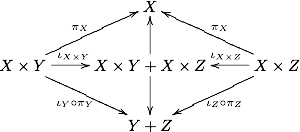
La propiedad universal para X×(Y+Z) garantiza un único morfismo X×Y+X×Z → X×(Y+Z),. Una categoría distributiva es aquella en el cual este morfismo es realmente un isomorfismo

$X\times (Y+Z)\simeq (X\times Y)+(X\times Z).$

Véase también

• Coproducto – la noción dual del producto
• Límites y colimites
• Igualador (teoría de categorías)
• Límite inverso
• Categoría cartesianamente cerrada
• producto fibrado (teoría de categorías)

Referencias

• Plantilla:Cita libro
• Plantilla:Cita libro Chapter 5.
• Plantilla:Cita libro

Enlaces externos

• Interactive Web page which generates examples of products in the category of finite sets. Written by Jocelyn Paine.