Deducción del módulo de la suma

Este artículo presenta una deducción para la expresión del módulo resultante de dos vectores (véase vector (física) y módulo (vector)) de un espacio vectorial (sobre los números reales).

Deducción

Sean dos vectores $\overrightarrow{a}$ y $\overrightarrow{b}$ que forman un ángulo $\theta$ entre sí:

Imagen de vectores colocados

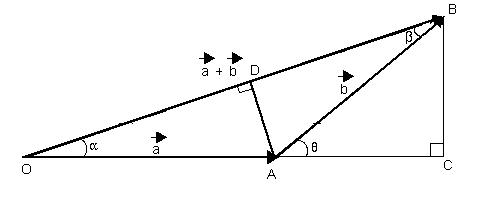
La fórmula para calcular $|\overrightarrow{a}+\overrightarrow{b}|$ se deduce observando los triángulos rectángulos que se forman, OCB y ACB, y aplicando el Teorema de Pitágoras. En el triángulo OCB: Plantilla:Ecuación Resultando: Plantilla:Ecuación En el triángulo ACB : Plantilla:Ecuación Sustituyendo esto en la igualdad de antes resulta:

${|\overrightarrow{a}+\overrightarrow{b}|}^2={(|\overrightarrow{a}|+|\overrightarrow{b}|\cos \theta )}^2+{(|\overrightarrow{b}|\sin \theta )}^2$

${|\overrightarrow{a}+\overrightarrow{b}|}^2=|\overrightarrow{a}{|}^2+2|\overrightarrow{a}||\overrightarrow{b}|\cos \theta +|\overrightarrow{b}{|}^2{\cos }^2\theta +|\overrightarrow{b}{|}^2{\sin }^2\theta$

${|\overrightarrow{a}+\overrightarrow{b}|}^2=|\overrightarrow{a}{|}^2+2|\overrightarrow{a}||\overrightarrow{b}|\cos \theta +|\overrightarrow{b}{|}^2({\cos }^2\theta +{\sin }^2\theta )$

${\cos }^2\theta +{\sin }^2\theta =1\Rightarrow {|\overrightarrow{a}+\overrightarrow{b}|}^2=|\overrightarrow{a}{|}^2+2|\overrightarrow{a}||\overrightarrow{b}|\cos \theta +|\overrightarrow{b}{|}^2$

$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{|\overrightarrow{a}{|}^2+2|\overrightarrow{a}||\overrightarrow{b}|\cos \theta +|\overrightarrow{b}{|}^2}$

$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{|\overrightarrow{a}{|}^2+|\overrightarrow{b}{|}^2+2|\overrightarrow{a}||\overrightarrow{b}|\cos \theta }$

Plantilla:Control de autoridades