Descomposición de una aplicación lineal

Isomorfismo canónico

Definición y teorema

Sean $E$ y $F$ dos espacios vectoriales sobre un mismo cuerpo, o más generalmente, dos módulos sobre un mismo anillo. Sea $f$ una aplicación lineal, $N=\ker (f)$ su núcleo e $I=\text{Im}(f)$ su imagen o codominio.

Teorema: Existe un isomorfismo canónico $\varphi$:

$\begin{array}{cccc}\varphi :& E/N& ⟶& I\\ & \bar{a}& ⟼& f(a)\end{array}$

donde $\bar{a}=\hat{a}=a+N$ se puede ver como la clase de $a$ en $E/N$ ("a" módulo "N") o como el conjunto $a+N=\{a+n:n\in N\}$ de los elementos de la forma $a+n$ con $n\in N$.

Prueba

1. Primero hay que verificar que $\varphi$ está bien definida, porque se ha definido $\varphi (\hat{a})$ escogiendo un elemento $a$ (un representante) de la clase $\hat{a}$, y mirando su imagen por $f$. Hay que establecer que esta imagen no depende de esta elección.
   Sea entonces $u\in \hat{a}$ otro elemento de $\hat{a}$. Las clases de $a$ y $u$ son idénticas: $\hat{a}=\hat{u}$, lo que se puede escribir también: $a+N=u+N$. Entonces $u-a+N=N$, lo que significa que $u-a\in N$ (porque $n\in N$, luego $a-u+0$ también).
   Luego existe $n$ en el núcleo de $f$ tal que $u=a+n$, entonces $f(u)=f(a+n)=f(a)+f(n)=f(a)+0=f(a)$ por linealidad.
   
2. $\varphi$ es sobreyectiva: Todo elemento de la imagen $I$ es por definición de la forma $f(a)$ que vale $\varphi (\hat{a})$; luego pertenece también a $\text{Im}(\varphi )$.
   
3. $\varphi$ es inyectiva: $\varphi (\hat{a})=0$ significa que $f(a)=0$, es decir que $a\in N$. Entonces $\hat{a}=a+N=o+N=N=\hat{o}$ que es el elemento neutro de $E/N$.

$◻$

Descomposición de una aplicación lineal

Este isomorfismo se completa naturalmente en una descomposición de la aplicación lineal: $f=i\circ \varphi \circ \pi$, donde $i$ es la inclusión canónica de $I$ en $F$ ($i(x)=x$ para todo $x\in I$), y $\pi$ es la sobreyección canónica de $E$ sobre $E/N$ ($\pi (a)=\hat{a}$ para todo $a\in E$):

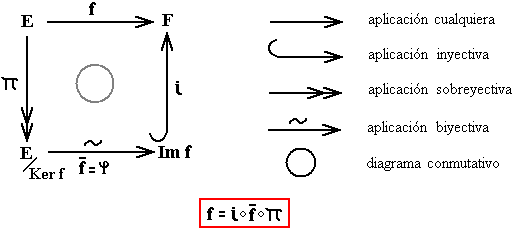
En efecto: $i\circ \varphi \circ \pi (a)=i\circ \varphi (\hat{a})=\varphi (\hat{a})=f(a)$ para todo $a\in E$.

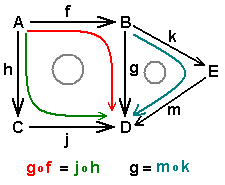
El diagrama precedente es conmutativo en el sentido siguiente:
Cuando existen dos caminos para ir de un punto a otro del diagrama, respetando claro está la orientación de las flechas, entonces se obtiene el mismo resultado por la composición de las aplicaciones.
En este nuevo ejemplo, los caminos verdes y rojos dan la misma aplicación: $g\circ f=j\circ h$ y el camino azul equivale al negro: $m\circ k=g$.

Ejemplos

1) Sea $f$ la aplicación que asocia a un entero $n$ su resto por la división euclidiana por 7 (escogido al azar).
Los restos posibles son 0, 1, 2, 3, 4, 5 y 6. La división de 6 por 7 da un resto de 6, mientras que la de 7 por 7 da como resto 0. Es por lo tanto lógico decidir que 0 sucede a 6 en este conjunto, que adquiere así una estructura circular. De hecho, se trata del anillo cíclico ${\mathbb{Z}}_7$:

${\mathbb{Z}}_7=\{\bar{0},\bar{1},\bar{2},\bar{3},\bar{4},\bar{5},\bar{6}\}$

, provisto de la adición módulo 7 y de la multiplicación también módulo 7.

La aplicación $f$ es lineal como propiedad de las congruencias, es sobreyectiva porque cada cifra entre 0 y 6 corresponde a un resto posible: basta con tomar el dividendo igual a la cifra.

No es inyectiva, y su núcleo es $\{...,-21,-21,-7,0,7,14,21...\}=7\mathbb{Z}$ porque los dividendos que dan restos nulos son claramente los múltiplos de 7.

Como la inclusión $i$ es, como $f$, sobreyectiva, se vuelve biyectiva (una inclusión es por definición inyectiva) y podemos prescindir de ella en la descomposición:

La flecha en diagonal representa el isomorfismo canónico entre $\mathbb{Z}/7\mathbb{Z}$ y ${\mathbb{Z}}_7$.

2) Consideremos el producto vectorial en ${ℝ}^3$, por un vector dado. Para fijar las cosas, sea $(𝐢,𝐣,𝐤)$ una base ortonormal directa del espacio usual, y estudiemos la aplicación que al vector $𝐮$ asocia el vector $𝐢\times 𝐮$ (el producto vectorial se denota $\times$ o $\wedge$, según los países).

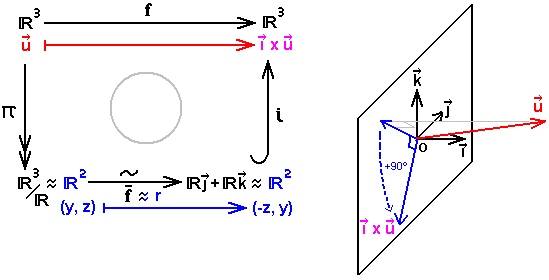
Su descomposición es la siguiente:
La sobreyección $\pi$ es asimilable a la proyección ortogonal sobre el plano $(Oyz)$ (mediante la identificación de una recta dirigida por $𝐢$ a su intersección con el plano anterior). En ella interviene la rotación $r$ directa de 90 grados en el plano $(Oyz)$ perpendicular al vector $𝐢$.
De hecho $\bar{f}$ es asimilable a $r$ (gracias a la identificación anterior).
Esto no es de extrañar porque el producto vectorial y las rotaciones en el espacio están íntimamente ligadas (ver cuaterniones y rotación en el espacio).