Estrofoide

Construcción de la estrofoide recta de polo X y de punto fijo O, tomando por curva base el eje Oy

En matemáticas, y más precisamente en geometría, una curva estrofoide, o simplemente una estrofoide, es una curva engendrada a partir de una curva dada $C$ y de dos puntos $A$ (el punto fijo) y $O$ (el polo).

En el caso particular en el que $C$ es una recta, $A$ pertenece a $C$, y $O$ no pertenece a $C$, la curva se denomina una estrofoide oblicua. Si, además, $OA$ es perpendicular a $C$, la curva es denominada una estrofoide recta, o simplemente una estrofoide por ciertos autores. La estrofoide recta a veces también se denomina curva logocíclica.

Construcción

Construcción de una estrofoide en el caso general

La curva estrofoidal que corresponde a la curva C, con el punto fijo A y el polo O se construye de la manera siguiente: sea L una recta móvil que pasa por O y que corta C en K. Sean entonces P₁ y P₂ los dos puntos de L tales que P₁K = P₂K = AK. El lugar geométrico de los puntos P₁ y P₂ se denomina la estrofoide de C relativa al polo O y con el punto fijo A. Se observa que AP₁ y AP₂ son ortogonales.

Ecuaciones

Coordenadas polares

Sea la curva $C$ dada por $r=f(\theta ),$, donde el origen se toma en $O$; y sea $A$ el punto de coordenadas cartesianas $(a,b)$. Si $K=(r\cos \theta ,r\mathrm{sen}\theta )$ es un punto de la curva, la distancia de $K$ a $A$ es

$d=\sqrt{(r\cos \theta -a{)}^2+(r\mathrm{sen}\theta -b{)}^2}=\sqrt{(f(\theta )\cos \theta -a{)}^2+(f(\theta )\mathrm{sen}\theta -b{)}^2}$

Los puntos de la recta $OK$ tienen por ángulo polar $\theta$, y los puntos a distancia $d$ de $K$ sobre esta recta están a una distancia $f(\theta )\pm d$ del origen. Por lo tanto, la ecuación de la estrofoide viene dada por

$r=f(\theta )\pm \sqrt{(f(\theta )\cos \theta -a{)}^2+(f(\theta )\mathrm{sen}\theta -b{)}^2}$

Coordenadas cartesianas

Sea $C$ de ecuaciones paramétricas $(x=x(t),y=y(t))$. Sea $A$ el punto $(a,b)$ y $O$ el punto $(p,q)$. Entonces, las fórmulas polares precedentes muestran que la representación paramétrica de la estrofoide es:

$x=u(t)=p+(x(t)-p)(1\pm n(t)),y=v(t)=q+(y(t)-q)(1\pm n(t))$

donde

$n(t)=\sqrt{\frac{(x(t)-a{)}^2+(y(t)-b{)}^2}{(x(t)-p{)}^2+(y(t)-q{)}^2}}$

Otra fórmula polar

La complejidad de las fórmulas precedentes limita su utilidad a la práctica. Existe por eso una forma alternativa a veces más sencilla, que es particularmente útil cuando $C$ es una sectriz de Maclaurin con polos $O$ y $A$.

Sea $O$ el origen y $A$ el punto $(a,0)$. Sea $K$ un punto de la curva, $\theta$ el ángulo entre $OK$ y el eje $OX$, y $\vartheta$ el ángulo entre $AK$ y el eje $OX$. Se supone que $\vartheta$ se da en función de $\theta$, bajo la forma $\vartheta =l(\theta )$. Sea el ángulo $\psi$ en $K$ tal que $\psi =\vartheta -\theta$. Entonces, se puede determinar $r$ en función de $l$ usando el teorema de los senos:

$\frac{r}{\mathrm{sen}\vartheta }=\frac{a}{\mathrm{sen}\psi },r=a\frac{\mathrm{sen}\vartheta }{\mathrm{sen}\psi }=a\frac{\mathrm{sen}l(\theta )}{\mathrm{sen}(l(\theta )-\theta )}$

Sean $P_1$ y $P_2$ los puntos de la recta $OK$ a la distancia $AK$ de $K$, numerados de forma que $\psi =\widehat{P_{1}Ka}$ y $\pi -\psi =\widehat{Ak{p}_2}$. El triángulo $P_{1}KA$ es isósceles de ángulo $\psi$ en el vértice, y por lo tanto los ángulos de la base $\widehat{A{P}_{1}K}$, y $\widehat{KA{P}_1}$ valen $(\pi -\psi )/2$. El ángulo entre $A{P}_1$ y el eje $OX$ es entonces

$l_1(\theta )=\vartheta +\mathrm{\angle }KA{P}_1=\vartheta +(\pi -\psi )/2=\vartheta +(\pi -\vartheta +\theta )/2=(\vartheta +\theta +\pi )/2$

Empleando el hecho de que $A{P}_1$ y $A{P}_2$ son perpendiculares (puesto que el triángulo $A{P}_1{P}_2$ está inscrito en una semicircunferencia), el ángulo entre $A{P}_2$ y el eje $OX$ vale

$l_2(\theta )=(\vartheta +\theta )/2$

La ecuación polar de la estrofoide se deduce entonces de $l_1$ y $l_2$ según las fórmulas precedentes:

$r_1=a\frac{\mathrm{sen}{l}_1(\theta )}{\mathrm{sen}(l_1(\theta )-\theta )}=a\frac{\mathrm{sen}((l(\theta )+\theta +\pi )/2)}{\mathrm{sen}((l(\theta )+\theta +\pi )/2-\theta )}=a\frac{\cos ((l(\theta )+\theta )/2)}{\cos ((l(\theta )-\theta )/2)}$

$r_2=a\frac{\mathrm{sen}{l}_2(\theta )}{\mathrm{sen}(l_2(\theta )-\theta )}=a\frac{\mathrm{sen}((l(\theta )+\theta )/2)}{\mathrm{sen}((l(\theta )+\theta )/2-\theta )}=a\frac{\mathrm{sen}((l(\theta )+\theta )/2)}{\mathrm{sen}((l(\theta )-\theta )/2)}$

$C$ es una sectriz de Maclaurin de polos $O$ y $A$ cuando $l$ es de la forma $q\theta +{\theta }_0$. En este caso, $l_1$ y $l_2$ tienen la misma forma, y la estrofoide es o bien otra sectriz de Maclaurin, o bien una pareja de sectrices. Se puede encontrar una ecuación polar sencilla si se toma el origen en el punto simétrico de $A$ respecto de $O$.

Casos particulares

Estrofoides oblicuas

Sea $C$ una recta que pasa por $A$. Entonces, en las notaciones precedentes, $l(\theta )=\alpha$ (donde $\alpha$ es una constante); y $l_1(\theta )=(\theta +\alpha +\pi )/2$ y $l_2(\theta )=(\theta +\alpha )/2$. Las ecuaciones polares de la estrofoide correspondiente con el origen en $O$, denominada estrofoide oblicua, toman la forma

$r=a\frac{\cos ((\alpha +\theta )/2)}{\cos ((\alpha -\theta )/2)}$

y

$r=a\frac{\mathrm{sen}((\alpha +\theta )/2)}{\mathrm{sen}((\alpha -\theta )/2)}$

Se verifica fácilmente que estas dos ecuaciones describen de hecho la misma curva.

Tomando el origen en $A$ (véase el artículo sobre la sectriz de Maclaurin) y reemplazando $-a$ por $a$, se obtiene

$r=a\frac{\mathrm{sen}(2\theta -\alpha )}{\mathrm{sen}(\theta -\alpha )}$

Una rotación de valor $\alpha$ transforma esta ecuación en

$r=a\frac{\mathrm{sen}(2\theta +\alpha )}{\mathrm{sen}(\theta )}$

En coordenadas cartesianas (y cambiando las constantes), se obtiene

$y(x^2+y^2)=b(x^2-y^2)+2cxy$

El resultado es una cúbica unicursal según su ecuación polar. Posee una singularidad en $(0,0)$, y la recta $y=b$ es una asíntota.

Estrofoide recta

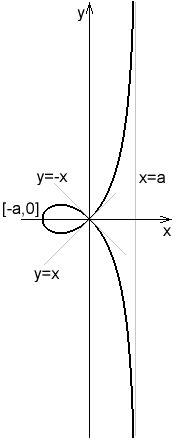
Estrofoide recta

Poniendo $\alpha =\pi /2$ en

$r=a\frac{\mathrm{sen}(2\theta -\alpha )}{\mathrm{sen}(\theta -\alpha )}$

se obtiene

$r=a\frac{\cos 2\theta }{\cos \theta }=a(2\cos \theta -\sec \theta )$

Esta curva se denomina estrofoide recta, y corresponde al caso donde $C$ es el eje $OY$, $O$ es el origen, y $A$ es el punto $(a,0)$.

Su ecuación cartesiana es

$y^2=x^2(a-x)/(a+x)$

y su representación paramétrica unicursal es:

$x=-a\frac{1-t^2}{1+t^2}$

$y=-at\frac{1-t^2}{1+t^2}$

La curva se asemeja al folium de Descartes, y la recta $x=-a$ es asíntota de las dos ramas infinitas. La curva posee dos asíntotasimaginarías más en el plano complejo, dadas por

$x\pm iy=-a$

Estrofoides de circunferencias que pasan por puntos fijos

Sea $C$ una circunferencia que pasa por $O$ y por $A$. Tomando $O$ por origen y $A$ en $(a,0)$, con las notaciones precedentes $l(\theta )=\alpha +\theta$ (donde $\alpha$ es una constante), se tiene que $l_1(\theta )=\theta +(\alpha +\pi )/2$ y que $l_2(\theta )=\theta +\alpha /2$. Entonces, las ecuaciones polares de las estrofoides correspondientes son

$r=a\frac{\cos (\theta +\alpha /2)}{\cos (\alpha /2)}$

y

$r=a\frac{\mathrm{sen}(\theta +\alpha /2)}{\mathrm{sen}(\alpha /2)}$

Son las ecuaciones de dos circunferencias que pasan también por $O$ y $A$, y forman ángulos de $\pi /4$ con $C$ en estos puntos.

Véase también

• Cisoide de Diocles
• Concoide de Durero
• Curvas
• Trisectriz de Maclaurin

Enlaces externos

• Al sitio web de Robert Ferreol, a su enciclopedia de las formas matemáticas destacables:
  • "Courbe Strophoïdale"
  • "estrofoide"
  • "estrofoide Droite", donde también se encuentran muchas propiedades geométricas de esta curva.

• Al sitio web de Mathworld
  • Plantilla:MathWorld, Eric W., Plantilla:MathWorld Plantilla:MathWorld Plantilla:MathWorld (Plantilla:MathWorld).
  • Plantilla:MathWorld, Eric W., Plantilla:MathWorld Plantilla:MathWorld Plantilla:MathWorld (Plantilla:MathWorld).