Función inversa

Una función ƒ y su función inversa ƒ^–1. Como ƒ aplica a en 3, la función inversa ƒ^–1 retorna 3 en a.

En matemáticas, especialmente en análisis matemático, si f es una función que asigna elementos de I en elementos de J, en ciertas condiciones será posible definir la función f ^-1 que realice el camino de vuelta de J a I. En ese caso diremos que f ^-1 es la función completamente opuesta a la original inversa de f.

Definiciones formales

Sea $f$ una función real biyectiva cuyo responsable o dominio sea el conjunto $I$ y cuya imagen sea el conjunto $J$. Entonces, la función inversa de $f$, denotada $f^{-1}$, es la función de dominio $J$ y codominio $I$ definida por la siguiente regla:

$f(x)=y\iff f^{-1}(y)=x\text{.}$

Destaquemos que $f^{-1}$, al igual que $f$, es una aplicación biyectiva, que queda determinada de modo único por $f$ y que cumple:

• $f^{-1}\circ f={\mathrm{id}}_i$ y
• $f\circ f^{-1}={\mathrm{id}}_j$.

De hecho, estas dos últimas propiedades caracterizan a la función inversa, como muestra la siguiente definición alternativa.

Definiciones alternativas

Dadas dos aplicaciones y las propiedades:

1. $g\circ f={\mathrm{id}}_I$ y
2. $f\circ g={\mathrm{id}}_J$,

entonces:

• Si se cumple 1) entonces $f$ es inyectiva y $g$ sobreyectiva, y diremos que $g$ es inversa por la izquierda de $f$.
• Si se cumple 2) entonces $g$ es inyectiva y $f$ sobreyectiva, y diremos que $g$ es inversa por la derecha de $f$.
• Si se cumplen simultáneamente 1) y 2) entonces $f$ y $g$ son biyectivas y $g$ es la inversa de $f$.

Este último punto se usa como definición de función inversa.

Notación alternativa

La notación tradicional $f^{-1}$ puede ser confusa, ya que puede dar a entender $\frac{1}{f}$ . Una notación alternativa utilizada en teoría de conjuntos es usar una estrella:

• $f^{\star }:B\to A$

Otra notación menos usada es utilizar solo el signo menos en vez del número $-1$:

• $f^{-}:B\to A$.

Propiedades algebraicas

Inversión del orden en la composición de funciones.

• La función inversa de la composición de dos funciones, siempre que tengan su función inversa, viene dada por la fórmula

$(g\circ f{)}^{-1}=f^{-1}\circ g^{-1}$

Obsérvese que se invierte el orden de f y g, pues para deshacer el camino avanzado primero por f y después por g, habrá que empezar deshaciendo este último por medio de g^–1 y terminar con f^–1,

• La involución: la función inversa de la función inversa de la función f , si existe, es la misma función f.

${\left(f^{-1}\right)}^{-1}=f$

Esta propiedad se deduce de la simetría que hay en las fórmulas: $f^{-1}\circ f={\mathrm{id}}_X$ y $f\circ f^{-1}={\mathrm{id}}_Y$.

Propiedades analíticas de funciones reales de una variable

Continuidad

• $f$ y $f^{-1}$ son simultáneamente continuas: Si una lo es, también lo será la otra. Sin embargo, es posible que ninguna lo sea: Por ejemplo se puede definir $f$ así: si $x$ es racional, $f(x)=x$, y si es irracional, $f(x)=-x$. En este caso muy particular $f=f^{-1}$.

• Además, en tal caso $f$ y $f^{-1}$ son monótonas y tienen el mismo sentido de variación (ver la figura).
  

Gráfica de la función inversa

Ejemplo de una función f y de su recíproca g, donde los respectivos dominios de definición son I = [ -6; 6 ] y J = [ -6 ; 2.

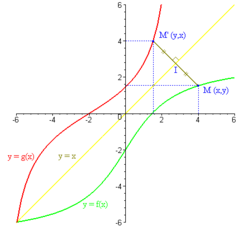
• Las gráficas que representan $f$ y $g=f^{-1}$ son simétricas con relación a la primera diagonal, es decir, la recta $y=x$. En efecto, esta simetría envía un punto cualquiera $M(x,y)$ sobre el punto $M^{\prime }(y,x)$. $M$ pertenece a la curva de $f$ si y sólo si $M^{\prime }$ pertenece a la de $g$, porque la primera condición se escribe $y=f(x)$ y la segunda $x=g(y)$ y son por definición equivalentes.

• Las tangentes en $M$ y $M^{\prime }$ tienen pendientes inversas. Es un efecto de la simetría anterior, y es la ilustración geométrica de la relación ya vista $g^{\prime }(y)f^{\prime }(x)=1$.

Derivación

• f y g son simultáneamente derivables: Si una lo es, también lo será la otra, con tal de aceptar valores infinitos de las derivadas de f y g.

• Además, en tal caso, para cualquier x de I, si notamos y = f(x), entonces por regla de la cadena tenemos que g'(y)· f'(x) = 1. La derivada de g se obtiene así fácilmente a partir de la de f (vean los ejemplos al final).

Ejemplos

En un sistema de coordenadas cartesianas se han representado las curvas de algunas raíces, así como de sus potencias, en el intervalo [0,1]. La diagonal, de ecuación y = x, es eje de simetría entre cada curva y la curva de su inversa.

• Por construcción misma, la función raíz cuadrada es función inversa de función cuadrática , con dominio restringido a los números reales no negativos, $x\to x^2$ Es decir, cada una de las dos funciones siguientes son una función inversa de la otra:

• Más generalmente, la función raíz positiva de orden n de un número positivo es la función inversa de la función potencia definida por $x\to x^n$.
• También por construcción, la función exponencial es la función inversa de la función logaritmo natural.
• Por definiciones muy adecuadas, arccos, arcsen y arctan son las funciones inversas de las funciones trigonométricas coseno, seno y tangente, lo que facilita hallar sus derivadas:

Para $f(x)=\cos (x)=y$, $g(y)=f^{-1}(y)=\arccos (y)$, y utilizando ${\cos }^2(x)+{\sin }^2(x)=1$ se obtiene: $g^{\prime }(y)=\frac{1}{f^{\prime }(x)}=\frac{1}{-\sin (x)}=\frac{1}{-\sqrt{1-{\cos }^2(x)}}=\frac{-1}{\sqrt{1-y^2}}$

Para $f(x)=\tan (x)=y$, $g(y)=f^{-1}(y)=\arctan (y)$, y utilizando ${\tan }^{\prime }(x)=1+{\tan }^2(x)$ se obtiene: $g^{\prime }(y)=\frac{1}{f^{\prime }(x)}=\frac{1}{1+{\tan }^2(x)}=\frac{1}{1+y^2}$

Se generaliza el concepto de función a otros conjuntos de números, en particular a los complejos, donde el logaritmo (con un dominio restringido) y la exponencial siguen siendo funciones inversas.

• En otras ocasiones una función inversa puede existir y estar bien definida pero no puede escribirse en términos de funciones elementales, como sucede con la función f:

Plantilla:Ecuación Aunque la función inversa se puede aproximar mediante desarrollo en serie de Taylor: Plantilla:Ecuación

Véase también

• Teorema de la función inversa, condiciones suficientes para la existencia de una función inversa continua y diferenciable.

Referencias

Bibliografías

• Bartle, Robert Galvis -Sherbert, Donald R. Introducción al Análisis matematemático de una variable, Noriega Editores, México 1984.
• Oubiña,Lía : Introducción a la teoría de conjuntos, Eudeba, Buenos Aires.