Lámina plana

En física, la definición matemática de una lámina plana consiste en un conjunto cerrado en un plano de masa $m$ y una densidad de superficie $\rho (x,y)$ tal que:

$m=\int \underset{}{\int }\rho (x,y)dxdy$, sobre el conjunto cerrado.

El centro de masas de la lámina está en el punto

$(\frac{M_y}{m},\frac{M_x}{m})$

donde $M_y$ es el momento de toda la lámina sobre el eje xy; y $M_x$ es el momento de toda la lámina sobre el eje y.

$M_y=\underset{m,n\to \mathrm{\infty }}{\lim }\sum _{i=1}^m\sum _{j=1}^{n}x{{}_{ij}}^{*}\rho (x{{}_{ij}}^{*},y{{}_{ij}}^{*})\mathrm{\Delta }\mathrm{A}=\underset{}{\iint }x\rho (x,y)dxdy$, sobre la superficie cerrada.

$M_x=\underset{m,n\to \mathrm{\infty }}{\lim }\sum _{i=1}^m\sum _{j=1}^{n}y{{}_{ij}}^{*}\rho (x{{}_{ij}}^{*},y{{}_{ij}}^{*})\mathrm{\Delta }\mathrm{A}=\underset{}{\iint }y\rho (x,y)dxdy$, sobre la superficie cerrada.

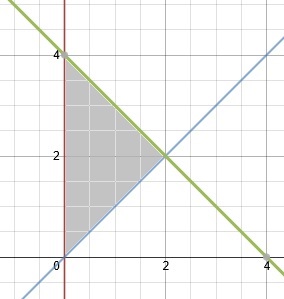
Ejemplo 1. Encuéntrese el centro de masa de una lámina con los bordes dados por las líneas $x=0,$ $y=x$ y $y=4-x$ donde la densidad se da como $\rho (x,y)=2x+3y+2$.

$m=\underset{0}{\overset{2}{\int }}{\underset{x}{\overset{4-x}{\int }}}_{}(2x+3y+2)dydx$

Integrar 2x + 3y + 2 con respecto a y; y sustituir los límites 4-x y x

$m=\underset{0}{\overset{2}{\int }}(2xy+\frac{3y^2}{2}+2y){|}_x^{4-x}dx$

$m=\underset{0}{\overset{2}{\int }}\left(\right[2x(4-x)+\frac{3(4-x{)}^2}{2}+2(4-x)]-[2x(x)+\frac{3(x{)}^2}{2}+2(x)\left]\right)dx$

$m=\underset{0}{\overset{2}{\int }}(8x-2x^2+\frac{3x^2-24x+48}{2}+8-2x-2x^2-\frac{3x^2}{2}-2x)dx$

$m=\underset{0}{\overset{2}{\int }}(8x-2x^2+\frac{3}{2}{x}^2-12x+24+8-2x-2x^2-\frac{3}{2}{x}^2-2x)dx$

$m=\underset{0}{\overset{2}{\int }}(-4x^2-8x+32)dx$

$m=(-\frac{4x^3}{3}-4x^2+32x){|}_0^2$

$m=\frac{112}{3}$

$M_y=\underset{0}{\overset{2}{\int }}\underset{x}{\overset{4-x}{\int }}x(2x+3y+2)dydx$

$M_y=\underset{0}{\overset{2}{\int }}(2x^{2}y+\frac{3x{y}^2}{2}+2xy){|}_x^{4-x}dx$

$M_y=\underset{0}{\overset{2}{\int }}(-4x^3-8x^2+32x)dx$

$M_y=(-x^4-\frac{8x^3}{3}+16x^2){|}_0^2$

$M_y=\frac{80}{3}$

$M_x=\underset{0}{\overset{2}{\int }}\underset{x}{\overset{4-x}{\int }}y(2x+3y+2)dydx$

$M_x=\underset{0}{\overset{2}{\int }}(x{y}^2+y^3+y^2){|}_x^{4-x}dx$

$M_x=\underset{0}{\overset{2}{\int }}(-2x^3+4x^2-40x+80)dx$

$M_x=(-\frac{x^4}{2}+\frac{4x^3}{3}-20x^2+80x){|}_0^2$

$M_x=\frac{248}{3}$

el centro de masa está en el punto

$(\frac{\frac{80}{3}}{\frac{112}{3}},\frac{\frac{248}{3}}{\frac{112}{3}})=(\frac{5}{7},\frac{31}{14})$

Las láminas planas se pueden usar para determinar momento de inercia, o centros de masa.