Prueba de Garfield del teorema de Pitágoras

Garfield en 1881

La prueba de Garfield del teorema de Pitágoras es una prueba original del teorema de Pitágoras inventada por James A. Garfield (19 de noviembre de 1831 - 19 de septiembre de 1881), vigésimo presidente de los Estados Unidos. La prueba apareció impresa en el New-England Journal of Education (Vol. 3, No.14, 1 de abril de 1876). Cuando se publicó la prueba Garfield no era el Presidente, sólo era el Congresista por Ohio. Asumió el cargo de Presidente el 4 de marzo de 1881, y sirvió en esa posición sólo por un breve período hasta el 19 de septiembre de 1881. Garfield ha sido el único Presidente de Estados Unidos que ha aportado algo novedoso a las matemáticas. La demostración no es trivial y, según el historiador de matemáticas William Dunham, «la de Garfield es realmente una demostración muy inteligente». La prueba aparece como la 231ª prueba en La proposición pitagórica, un compendio de 370 pruebas diferentes del teorema de Pitágoras.

La prueba

Diagrama para explicar la prueba de Garfield del teorema de Pitágoras

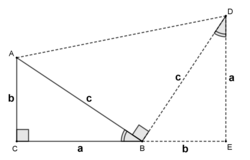
En la figura, $ABC$ es un triángulo rectángulo con ángulo recto en $C$. Los lados del triángulo son $a,b,c$. El teorema de Pitágoras afirma que $c^2=a^2+b^2$.

Para demostrar el teorema, Garfield trazó una línea a través de $B$ perpendicular a $AB$ y en esta línea elegir un punto $D$ de tal forma que $BD=BA$. A continuación, desde $D$ dejó caer una perpendicular $DE$ sobre la línea extendida $CB$. En la figura se puede ver fácilmente que los triángulos $ABC$ y $BDE$ son congruentes. Desde $AC$ y $DE$ son ambos perpendiculares a $CE$, son paralelas y por tanto el cuadrilátero $ACED$ es un trapezoide. El teorema se demuestra calculando el área de este trapecio de dos formas distintas.

$\begin{array}{cc}\text{área del trapezoide }ACED& =\text{altura }\times \text{media de lados paralelos }\\ & =CE\times \frac{1}{2}(AC+DE)=(a+b)\times \frac{1}{2}(a+b)\end{array}$.

$\begin{array}{cc}\text{área del trapezoide}ACED& =\text{área de}\mathrm{\Delta }ACB+\text{área de}\mathrm{\Delta }ABD+\text{área de }\mathrm{\Delta }BDE\\ & =\frac{1}{2}(a\times b)+\frac{1}{2}(c\times c)+\frac{1}{2}(a\times b)\end{array}$

De ellos se obtiene

$(a+b)\times \frac{1}{2}(a+b)=\frac{1}{2}(a\times b)+\frac{1}{2}(c\times c)+\frac{1}{2}(a\times b)$

lo que simplificando da como resultado

$a^2+b^2=c^2$