Superfórmula

Algunos ejemplos de superfórmula. Son mostradas en la imagen para a=b=1 y para los: m, n1, n2 y n3; indicados.

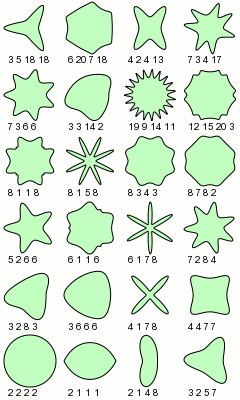
La superfórmula es una generalización en coordenadas polares de la superelipse, propuesta por Johan Gielis.

Gielis supuso que la fórmula puede ser usada para describir distintas curvas y cuerpos presentes en la Naturaleza.

La fórmula es:

$r\left(\phi \right)={({\left|\frac{cos\left(\frac{m\phi }{4}\right)}{a}\right|}^{n_2}+{\left|\frac{sin\left(\frac{m\phi }{4}\right)}{b}\right|}^{n_3})}^{-\frac{1}{n_1}}$

donde $r$ es el radio y $\phi$ el ángulo.

La fórmula apareció en abril de 2003, en el número 90 de la revista American Journal of Botany, en un artículo del biólogo Johan Gielis. Fue obtenida generalizando la superelipse, creada por el matemático danés Piet Hein.

Extensión a dimensiones superiores

Es posible ampliar esta fórmula a n dimensiones, multiplicando las superfórmulas entre sí. Por ejemplo, la superficie paramétrica de tres dimensiones se puede obtener multiplicando dos de ellas:

$x=r_1(\theta )\cos (\theta )r_2(\varphi )\cos (\varphi )$

$y=r_1(\theta )\sin (\theta )r_2(\varphi )\cos (\varphi )$

$z=r_2(\varphi )\sin (\varphi )$

donde φ varía entre -π/2 y π/2 (latitud), y θ entre -π y π (longitud).

Gráficas por ordenador

Podemos ver un ejemplo de representación gráfica, en un lenguaje como scilab, con la que podemos obtener una representación en 2D de esta función:

// 'b'-blue,    'c'-cyan, 'g'-green, 'k'-blak,
// 'm'-magenta, 'r'-red,  'w'-white, 'y'-yelow.

scf(0);
clf(0);

esc=1;
n=2; // rotaciones
a=5; b=1; m=1; n1=2; n2=1; n3=1;

plot ([-4*esc,4*esc],[0,0],"c"); // eje x
plot ([0,0],[-3*esc,3*esc],"c"); // eje y

xtitle ("Superfórmula: n="+string(n)+"; a="+string(a)+", b="+string(b)+", m="+string(m)+", n1="+string(n1)+", n2="+string(n2)+", n3="+string(n3)+".");

t=linspace (0,2*n*%pi,1000);
r=(abs(cos(m*t/4)/a).^n2+abs(sin(m*t/4)/b).^n3).^(-1/n1);
x=r.*cos(t);
y=r.*sin(t);
plot (x,y,'g');

Enlaces externos

• Superfórmulas (en inglés)
• Supershapes (Superformula) (en inglés)