Bitruncamiento

En geometría, un bitruncamiento (o también bitruncación o bitruncado) es una operación definida sobre politopos regulares.[1] Representa un truncamiento más allá de la rectificación. Las aristas originales se eliminan por completo y las caras originales permanecen como copias más pequeñas de sí mismas.
Los politopos regulares bitruncados se pueden representar mediante una notación extendida de los símbolos de Schläfli Plantilla:Math o Plantilla:Math Plantilla:ContenidoPlantilla:Clear
En poliedros regulares y teselados
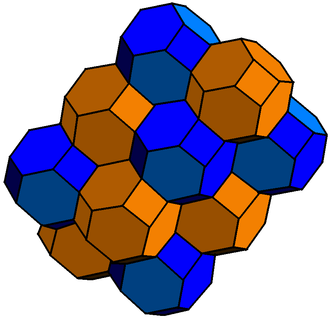
Para poliedros regulares (es decir, 3-politopos regulares), una forma bitruncada es la forma dual truncada. Por ejemplo, un cubo bitruncado es un octaedro truncado.
En 4-politopos regulares y panales
Para un polícoro normal, una forma bitruncada es un operador dual-simétrico. Un 4-politopo bitruncado es lo mismo que el dual bitruncado y tendrá el doble de simetría si el 4-politopo original es autodual.
Un politopo regular (o panal) {p, q, r} tendrá sus celdas {p, q} bitruncadas en celdas {q, p} truncadas, y los vértices se reemplazarán por celdas {q, r} truncadas.
4-politopos/panales {p,q,p} autoduales
Un resultado interesante de esta operación es que los 4-politopos autoduales {p,q,p} (y los panales) continúan siendo celdas-transitivos después del bitruncamiento. Hay cinco formas de este tipo correspondientes a los cinco poliedros regulares truncados: t{q,p}. Dos son panales en la 3-esfera, uno es un panal en el espacio tridimensional euclídeo y dos son panales en el espacio tridimensional hiperbólico.
| Espacio | 4-politopo o panal | Símbolo de Schläfli Diagrama de Coxeter-Dynkin |
Tipo de celda | Imagen de la celda |
Figura de vértice |
|---|---|---|---|---|---|
| 5-celdas bitruncado (10-celdas) (4-politopo uniforme) |
t1,2{3,3,3} Plantilla:DCD |
Tetraedro truncado | 
|

| |
| 24-celdas bitruncado (48-celdas) (4-politopo uniforme) |
t1,2{3,4,3} Plantilla:DCD |
Cubo truncado | 
|

| |
| Panal cúbico bitruncado (Panal convexo euclídeo uniforme) |
t1,2{4,3,4} Plantilla:DCD |
Octaedro truncado | 
|

| |
| Panal icosaédrico bitruncado (Panal convexo hiperbólico uniforme) |
t1,2{3,5,3} Plantilla:DCD |
Dodecaedro truncado | 
|

| |
| Panal dodecaédrico de orden 5 bitruncado (Panal convexo hiperbólico uniforme) |
t1,2{5,3,5} Plantilla:DCD |
Icosaedro truncado | 
|

|
Véase también
Plantilla:Portal Plantilla:Portal
Referencias
Bibliografía
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, Plantilla:ISBN (pp. 145–154 Chapter 8: Truncation)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Norman Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, Plantilla:ISBN (Chapter 26)