Distribución de Pareto

En teoría de la probabilidad y en estadística, la distribución Pareto es una distribución de probabilidad continua con dos parámetros, que tiene aplicación en disciplinas como la sociología, la geofísica y la economía. Fue formulada por el ingeniero civil, economista y sociólogo Vilfredo Pareto, aunque en ciertas áreas de estudio se hace referencia a la ley de Bradford. Cabe señalar que el equivalente discreto de la distribución Pareto es la distribución zeta (la ley de Zipf).

Cuando la distribución de Pareto es usada en un modelo sobre la distribución de riqueza, el parámetro $\alpha$ es conocido como índice de Pareto.

Definición

Notación

Si $X$ es una variable aleatoria continua con distribución Pareto con parámetros $\alpha >0$ y $x_m>0$ entonces escribimos $X\sim \mathrm{Pareto}(\alpha ,x_m)$.

Función de densidad

La función de densidad de una variable aleatoria $X\sim \mathrm{Pareto}(\alpha ,x_m)$ es

$f_X(x)=\frac{\alpha x_m^{\alpha }}{x^{\alpha +1}}$

para $x_m\le x$.

Probabilidad acumulada

La función de distribución de una variable aleatoria $X\sim \mathrm{Pareto}(\alpha ,x_m)$ es, para $x_m\le x$,

$F_X(x)=1-{\left(\frac{x_m}{x}\right)}^{\alpha }$

Propiedades

Si $X\sim \mathrm{Pareto}(\alpha ,x_m)$ entonces la variable aleatoria $X$ satisface algunas propiedades.

Media

La media de la variable aleatoria $X$ es

$\mathrm{E}[X]=\frac{\alpha x_{\mathrm{m}}}{\alpha -1}$

con $\alpha >1$.

Varianza

La varianza de la variable aleatoria $X$

$\mathrm{V}\mathrm{a}\mathrm{r}(X)=\frac{\alpha x_m^2}{(\alpha -1{)}^2(\alpha -2)}$

para $\alpha >2$.

Momentos

El $n$-ésimo momento sólo está definido para $n<\alpha$ y en tal caso es

$\mathrm{E}[X^n]=\frac{\alpha x_{\mathrm{m}}^n}{\alpha -n}$

Función generadora de momentos

La función generadora de momentos es

$M_X(t)=\alpha (-x_{\mathrm{m}}t{)}^{\alpha }\mathrm{\Gamma }(-\alpha ,-x_{\mathrm{m}}t)$

y está definida para valores $t<0$.

Caso degenerado

La función de la delta de Dirac es un caso límite de la densidad de Pareto:

$\underset{\alpha \to \mathrm{\infty }}{\lim }f(x;\alpha ,x_{\mathrm{m}})=\delta (x-x_{\mathrm{m}}).$

Distribución simétrica

Puede definirse una Distribución de Pareto Simétrica según:

$f(x;\alpha ,x_{\mathrm{m}})=\{\begin{array}{cc}(\alpha x_{\mathrm{m}}^{\alpha }/2)|x{|}^{-\alpha -1}& \text{si }|x|>x_{\mathrm{m}}\\ 0& \text{resto}.\end{array}$

Distribución Generalizada de Pareto

Plantilla:Ficha de distribución de probabilidad La familia de distribuciones generalizadas de Pareto (GPD) tienen tres parámetros $\mu ,\sigma$ y $\xi$.

La función de probabilidad acumulada es

$F_{(\xi ,\mu ,\sigma )}(x)=\{\begin{array}{cc}1-{(1+\frac{\xi (x-\mu )}{\sigma })}^{-1/\xi }& \text{si }\xi \ne 0,\\ 1-\exp (-\frac{x-\mu }{\sigma })& \text{si }\xi =0.\end{array}$

Para $x⩾\mu$, con $\xi ⩾0$, y $x⩽\mu -\sigma /\xi$ con $\xi <0$, donde $\mu \in ℝ$ es el parámetro localización, $\sigma >0$ es el parámetro escala y $\xi \in ℝ$ es el parámetro forma. Nótese que algunas referencias toman el parámetro forma como $\kappa =-\xi$.

La función de densidad de probabilidad es:

$f_{(\xi ,\mu ,\sigma )}(x)=\frac{1}{\sigma }{(1+\frac{\xi (x-\mu )}{\sigma })}^{(-\frac{1}{\xi }-1)}.$

o

$f_{(\xi ,\mu ,\sigma )}(x)=\frac{{\sigma }^{\frac{1}{\xi }}}{{(\sigma +\xi (x-\mu ))}^{\frac{1}{\xi }+1}}.$

de nuevo, para $x⩾\mu$, y $x⩽\mu -\sigma /\xi$ si $\xi <0$

Inferencia estadística

Estimación de parámetros

La función de verosimilitud para los parámetros de la distribución de Pareto α y x_m, dada una muestra independiente x = (x₁, x₂, ..., x_n), es

$L(\alpha ,x_{\mathrm{m}})=\prod _{i=1}^n\alpha \frac{x_{\mathrm{m}}^{\alpha }}{x_i^{\alpha +1}}={\alpha }^n{x}_{\mathrm{m}}^{n\alpha }\prod _{i=1}^n\frac{1}{x_i^{\alpha +1}}.$

Por lo tanto, la función de verosimilitud logarítmica es

$\ell (\alpha ,x_{\mathrm{m}})=n\ln \alpha +n\alpha \ln x_{\mathrm{m}}-(\alpha +1)\sum _{i=1}^n\ln x_i.$

Se puede ver que $\ell (\alpha ,x_{\mathrm{m}})$ es monotonamente ascendente con x_m, es decir, cuanto mayor es el valor de x_m, mayor es el valor de la función de verosimilitud. Por lo tanto, dado que x ≥ x_m, se concluye que

${\hat{x}}_{\mathrm{m}}=\underset{i}{\min }{x}_i.$

Para calcular el estimador de α, se calcula la derivada parcial correspondiente y se determina dónde es cero:

$\frac{\partial \ell }{\partial \alpha }=\frac{n}{\alpha }+n\ln x_{\mathrm{m}}-\sum _{i=1}^n\ln x_i=0.$

Por lo tanto el estimador de máxima verosimilitud para α ess:

$\hat{\alpha }=\frac{n}{\sum _i\ln (x_i/{\hat{x}}_{\mathrm{m}})}.$

El error estadístico esperado es:

$\sigma =\frac{\hat{\alpha }}{\sqrt{n}}.$

Malik (1970) da la distribución conjunta exacta de $({\hat{x}}_{\mathrm{m}},\hat{\alpha })$. En particular, ${\hat{x}}_{\mathrm{m}}$ y $\hat{\alpha }$ son independientes y ${\hat{x}}_{\mathrm{m}}$ es Pareto con parámetro de escala x_m y parámetro de forma nα, mientras que $\hat{\alpha }$ posee una distribución gama inversa con parámetros de forma y escala n − 1 y nα, respectivamente.

Ocurrencia y aplicaciones

General

Aplicación de la distribución de probabilidad acumulada de Pareto a lluvias diarias máximas.

Vilfredo Pareto utilizó originalmente esta distribución para describir la asignación de la riqueza entre los individuos, ya que parecía mostrar bastante bien la forma en que una mayor parte de la riqueza de cualquier sociedad es propiedad de un porcentaje menor de las personas de esa sociedad. También lo utilizó para describir la distribución de la renta. Esta idea se expresa a veces de forma más sencilla como el principio de Pareto o la "regla del 80-20", que dice que el 20% de la población controla el 80% de la riqueza. Sin embargo, la regla del 80-20 corresponde a un valor particular de α, y de hecho, los datos de Pareto sobre los impuestos británicos sobre la renta en su Cours d'économie politique indican que aproximadamente el 30% de la población tenía alrededor del 70% de los ingresos. La función de densidad de probabilidad (PDF) al principio de este artículo muestra que la "probabilidad" o fracción de la población que posee una pequeña cantidad de riqueza por persona es bastante alta, y luego disminuye constantemente a medida que aumenta la riqueza. (Sin embargo, la distribución de Pareto no es realista para la riqueza del extremo inferior. De hecho, el patrimonio neto puede ser incluso negativo). Esta distribución no se limita a describir la riqueza o la renta, sino muchas situaciones en las que se encuentra un equilibrio en la distribución de lo "pequeño" a lo "grande". Los siguientes ejemplos se consideran a veces como una distribución de Pareto aproximada:

• Los tamaños de los asentamientos humanos (pocas ciudades, muchas aldeas/pueblos)
• Distribución de los tamaños de los archivos del tráfico de Internet que utiliza el protocolo TCP (muchos archivos pequeños, pocos archivos grandes
• Tasas de error en los Unidades de disco duro
• Clusters de condensado de Bose-Einstein cerca del cero absoluto

Distribución acumulativa de Pareto (Lomax) ajustada a las precipitaciones máximas de un día utilizando CumFreq, véase también ajuste de distribución

• Los valores de las reservas de petróleo en los yacimientos petrolíferos (unos pocos grandes yacimientos, muchos pequeños yacimientos)
• La distribución de la longitud en los trabajos asignados a los superordenadores (unos pocos grandes, muchos pequeños)
• La rentabilidad estandarizada de los precios de las acciones individuales
• Los tamaños de las partículas de arena
• El tamaño de los meteoritos
• La gravedad de las grandes pérdidas por fallecimiento en el negocio de Seguros, para ciertas líneas de negocio como la responsabilidad civil general, el automóvil comercial y la compensación de los trabajadores.
• Cantidad de tiempo que un usuario en el servicio Steam pasará jugando a diferentes juegos. (Algunos juegos se juegan mucho, pero la mayoría no se juegan casi nunca) [1]
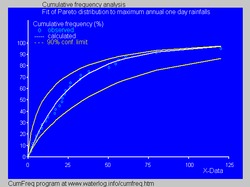
• En hidrología la distribución de Pareto se aplica a eventos extremos como las precipitaciones máximas anuales de un día y las descargas de los ríos. y además para describir épocas de sequía. La imagen azul ilustra un ejemplo de ajuste de la distribución de Pareto a las precipitaciones máximas anuales de un día clasificadas mostrando también la banda de confianza del 90% basada en la distribución binomial. Los datos de las precipitaciones se representan mediante posición de trazado como parte del análisis de la frecuencia acumulada.
• En la fiabilidad de la distribución de los servicios eléctricos (el 80% de los minutos de los clientes interrumpidos se producen en aproximadamente el 20% de los días de un año determinado).

Software

Se puede usar software y un programa de computadora para el ajuste de una distribución de probabilidad, incluyendo la de Pareto, a una serie de datos:

• Easy fit Plantilla:Wayback, "data analysis & simulation"
• ModelRisk, "risk modelling software"
• Ricci distributions, fitting distrubutions with R, Vito Ricci, 2005
• Risksolver, automatically fit distributions and parameters to samples
• StatSoft distribution fitting Plantilla:Wayback
• CumFreq, sin costo, incluye intervalos de confianza a base de la distribución binomial

Bibliografía

• Barry C. Arnold (1983). Pareto Distributions, International Co-operative Publishing House, Burtonsville, Maryland. ISBN 0-899974-012-1.
• Christian Kleiber and Samuel Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences, New York:Wiley. xi+332 pp. ISBN 0-471-15064-9.
• Lorenz, M. O. (1905). "Methods of measuring the concentration of wealth". Publications of the American Statistical Association. 9: 209–219.

Véase también

• Distribución de Weibull
• Ley de Bradford
• Ley de Gutenberg-Richter
• Efecto Mateo
• Eficiencia de Pareto
• Ley de Sturgeon
• Ley de Zipf

Enlaces externos

• Calculadora - Distribución de Pareto