Ángulos suplementarios

Ángulos suplementarios.

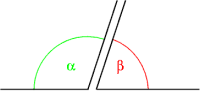
Dos ángulos son ángulos suplementarios si suman $180^{\circ }$. Así, se denomina a un ángulo "suplemento" de otro, si aquel es lo que le falta a este para medir un ángulo plano o llano.

Método de obtención

Aritmético

Para obtener el ángulo suplementario $\beta$ de un determinado ángulo $\alpha$, se restará $\alpha$ a $180^{\circ }$, de manera que:

$\beta =180^{\circ }-\alpha$

Propiedades

• Los ángulos que midan más que $180^{\circ }$ no tienen ángulo suplementario.Plantilla:Cita requerida

• El valor de $180^{\circ }$ es el mismo que dos ángulos rectos, $\pi$ rad, $\tau /2$ rad o $200^g$ grados centesimales.
• Si dos ángulos son suplementarios de otros dos ángulos congruentes, también son congruentes entre sí.
• Los senos de los ángulos suplementarios son los mismos, por ejemplo:

$\mathrm{sen}\alpha =\mathrm{sen}(180^{\circ }-\alpha )$

$\mathrm{sen}\alpha =\mathrm{sen}(\pi -\alpha )$

$\mathrm{sen}120^{\circ }=\mathrm{sen}60^{\circ }$

• Los cosenos de los ángulos suplementarios son de igual valor absoluto, pero de signo inverso, como muestran los siguientes ejemplos:

$\cos \alpha =-\cos (180^{\circ }-\alpha )$

$\cos \alpha =-\cos (\pi -\alpha )$

$\cos 120^{\circ }=-\cos 60^{\circ }$

Véase también

Relaciones aritméticas entre ángulos:

• Ángulos congruentes
• Ángulos complementarios
• Ángulos replementarios
• Ángulos explementarios

Relaciones posicionales entre ángulos:

• Ángulos adyacentes
• Ángulos consecutivos
• Ángulos opuestos por el vértice
• Ángulos interiores y exteriores

Determinados por dos paralelas y una transversal:

• Ángulos correspondientes
• Ángulos alternos externos e internos
• Ángulos conjugados externos e internos