Movimiento relativo

El movimiento siempre es un concepto relativo porque debe referirse a un sistema de referencia o sistema referencial particular escogido por el observador. Puesto que diferentes observadores pueden utilizar referenciales distintos, es importante relacionar las observaciones realizadas por aquellos. Una partícula se encuentra en movimiento en un referencial si su posición con respecto a él cambia en el transcurso del tiempo; en caso contrario, la partícula está en reposo en dicho referencial. De estas definiciones, vemos que tanto el concepto de movimiento como el de reposo son relativos. Así, el pasajero (B) que está sentado en un vagón de ferrocarril (C) se encuentra en reposo con respecto al vagón; pero como el tren se mueve con respecto a la Tierra, el pasajero se encuentra en movimiento con respecto a los árboles (A) que observa desde el tren. A su vez, esos árboles están en reposo respecto de la Tierra, pero en movimiento respecto del pasajero del tren. A efectos prácticos, podemos distinguir dos modalidades de movimiento relativo:

Diagrama, donde A representa al árbol, B al viajero y C al vagón.

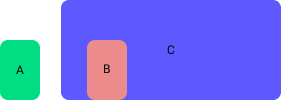
• Movimiento de una partícula en dos referenciales diferentes en movimiento relativo entre sí.
• Movimiento relativo entre dos partículas en un mismo referencial.

Movimiento de una partícula en dos referenciales

Sistema de referencia fijo o absoluto (XYZ) y sistema de referencia móvil o relativo (xyz) en movimiento general (rototraslatorio) respecto al referencial absoluto.

En este caso, el movimiento relativo hace referencia al que presenta una partícula con respecto a un sistema de referencia (ptp), llamado referencial relativo o fijo por estar en movimiento con respecto a otro sistema de referencia (XTV) considerado como referencial absoluto o móvil.

El movimiento de un referencial respecto al otro puede ser una traslación, una rotación o una combinación de ambas (movimiento rototraslatorio).

Velocidad

La velocidad ${𝐯}_{\text{F}}$ de una partícula en un referencial fijo o absoluto y su velocidad ${𝐯}_{\text{M}}$ en un referencial móvil o relativo están relacionadas mediante esta expresión:

siendo:

${𝐯}_{\text{F}}$ la velocidad de la partícula en el referencial fijo (velocidad absoluta).

${𝐯}_{\text{M}}$ la velocidad de la partícula en el referencial móvil (velocidad relativa),

${𝐯}_{\text{o}}$ la velocidad del origen del referencial móvil en el referencial fijo (arrastre de traslación),

$\mathit{\omega }$ la velocidad angular del referencial móvil respecto del referencial fijo (velocidad angular de arrastre),

$\mathit{\omega }\times 𝐫$ la velocidad de arrastre de rotación.

Los dos últimos términos representan la velocidad de arrastre total, de modo que podemos escribir

que coincide con la velocidad correspondiente a un punto de un sólido rígido en movimiento.

Podemos expresar la velocidad de la partícula en el referencial fijo en la forma

Aceleración

La aceleración ${𝐚}_{\text{F}}$ de una partícula en un referencial fijo o absoluto y su aceleración ${𝐚}_{\text{M}}$ en un referencial móvil o relativo están relacionadas mediante la expresión:

siendo:

${𝐚}_{\text{F}}$ la aceleración de la partícula en el referencial fijo (aceleración absoluta).

${𝐚}_{\text{M}}$ la aceleración de la partícula en el referencial móvil (aceleración relativa),

${𝐯}_{\text{M}}$ la velocidad de la partícula en el referencial móvil (velocidad relativa),

${𝐚}_{\text{o}}$ la aceleración del origen del referencial móvil en el referencial fijo (arrastre de traslación),

$\dot{\mathit{\omega }}\times 𝐫$ la aceleración tangencial (arrastre de rotación),

$\mathit{\omega }\times (\mathit{\omega }\times 𝐫)$ la aceleración normal o centrípeta (arrastre de rotación),

$2\mathit{\omega }\times {𝐯}_{\text{M}}$ la aceleración complementaria o aceleración de Coriolis.

Si la partícula se encuentra en reposo en el referencial móvil, esto es, si ${𝐯}_{\text{M}}=0$ y ${𝐚}_{\text{M}}=0$, su aceleración en el referencial fijo es la aceleración de arrastre, que viene dada por

que coincide con la aceleración correspondiente un punto de un sólido rígido en movimiento.

Podemos expresar la aceleración de la partícula en el referencial fijo en la forma

Traslación solamente

La aceleración de una partícula en un referencial fijo o absoluto ${𝐚}_{\text{F}}$ y en un referencial móvil o relativo, ${𝐚}_{\text{M}}$, están relacionadas mediante la expresión:

Solo rotación

La aceleración de una partícula en un referencial fijo o absoluto ${𝐚}_{\text{F}}$ y en un referencial móvil o relativo, ${𝐚}_{\text{M}}$, están relacionadas mediante la expresión:

Movimiento relativo entre dos partículas en un mismo referencial

Movimiento relativo entre dos partículas en movimiento respecto a un mismo sistema referencial xyz

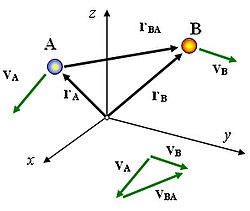
Consideremos dos partículas, A y B, que se mueven en el espacio y sean ${𝐫}_{\text{A}}$ y ${𝐫}_{\text{B}}$ sus vectores de posición con respecto al origen O de un referencial dado. Las velocidades de A y B medidas en ese referencial serán

Los vectores de posición (relativa) de la partícula B con respecto a la A y de la A con respecto a la B están definidos por

y las velocidades (relativas) de B con respecto a A y de A con respecto a B son

Puesto que ${𝐫}_{\text{BA}}=-{𝐫}_{\text{AB}}$, también resulta que ${𝐯}_{\text{BA}}=-{𝐯}_{\text{AB}}$, de modo que las velocidades relativas de B con respecto a A y de A con respecto a B son iguales y opuestas.

Efectuando las derivadas (3), resulta

o sea que

de modo que obtendremos la velocidad relativa entre las dos partículas restando vectorialmente sus velocidades con respecto a un mismo referencial (Oxyz en la figura).

Derivando de nuevo las expresiones (5) tenemos para las aceleraciones relativas

Los primeros miembros de (6) son las aceleraciones relativas de B con respecto a A y de A con respecto a B. Los otros términos son las aceleraciones de A y de B con respecto a un mismo observador Oxyz.

Tenemos Plantilla:Ecuación

siguiéndose para las aceleraciones relativas la misma regla que para las velocidades.

Véase también

• Velocidad relativa
• Aceleración relativa

Bibliografía

• Plantilla:Cita libro
• Plantilla:Cita libro
• Plantilla:Cita libro