Bitronco

Bitroncos
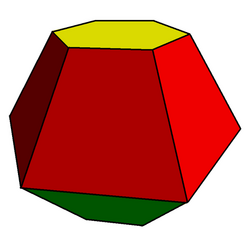Ejemplo: bitronco hexagonal
Caras	2 n-gonos, 2n trapecios
Aristas	5n
Vértices	3n
Grupo de simetría	Dnh, [n,2], (*n22)
Poliedro dual	Bipirámide elongada
Propiedades	Convexo

Un bitronco n-agonal es un poliedro que contiene tres n-ágonos planos paralelos, siendo el intermedio el más grande y generalmente el superior y el inferior congruentes entre sí.

Puede construirse como dos troncos congruentes combinados en un plano de simetría, y también como una bipirámide con los dos vértices polares truncados.

Son los poliedros duales de la familia de las bipirámides elongadas.

Fórmulas

Para un bitronco regular Plantilla:Mvar-gonal con las aristas del polígono ecuatorial de longitud Plantilla:Mvar, los lados de las bases Plantilla:Mvar y la semi-altura (la mitad de la distancia entre los planos de las bases) Plantilla:Mvar, el área de la superficie lateral Plantilla:Mvar, el área total Plantilla:Mvar y el volumen Plantilla:Mvar son:

$A_l=n(a+b)\sqrt{{(\frac{a-b}{2}\cot \frac{\pi }{n})}^2+h^2},$

$A=A_l+n\frac{b^2}{2\tan \frac{\pi }{n}},$

$V=n\frac{a^2-b^2}{6\tan \frac{\pi }{n}}h.$

Ejemplos

Tres bitroncos son los duales de tres sólidos de Johnson (J14, J15 y J16). En general, un bitronco n-agonal tiene 2n trapecios, 2 n-ágonos y es dual a una bipirámide elongada.

Bitronco triangular	Bitronco cuadrado	Bitronco pentagonal	Bitronco hexagonal
6 trapecios, 2 triángulos. Dual de la bipirámide triangular elongada, J14	8 trapecios, 2 cuadrados. Dual de la bipirámide cuadrada elongada, J15	10 trapecios, 2 pentágonos. Dual de la bipirámide pentagonal elongada, J16	12 trapecios, 2 hexágonos. Dual de la bipirámide hexagonal elongada, J17