Cúbica resolvente

Gráfico de la función polinómica Plantilla:Math (en verde) junto con el gráfico de su cúbica resolvente Plantilla:Math (en rojo). Las raíces de ambos polinomios también son visibles

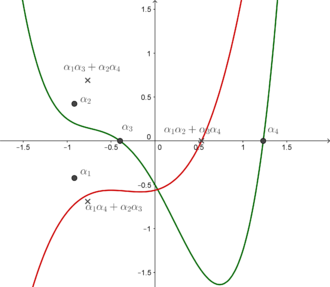
En álgebra, una ecuación cúbica resolvente es uno de varios polinomios cúbicos distintos, aunque relacionados, definidos a partir de un polinomio mónico de grado cuatro:

$P(x)=x^4+a_1{x}^3+a_2{x}^2+a_{3}x+a_4$

En cada caso:

• Los coeficientes de la cúbica resolvente se pueden obtener a partir de los coeficientes de $P(x)$ utilizando solo sumas, restas y multiplicaciones.
• Conocer las raíces de la cúbica resolvente de $P(x)$ es útil para encontrar las propias raíces de $P(x)$. De ahí el nombre de "cúbica resolvente".
• El polinomio $P(x)$ tiene una raíz múltiple si y solo si su cúbica resolvente tiene una raíz múltiple.

Definiciones

Supóngase que los coeficientes de $P(x)$ pertenecen a un cuerpo $k$ cuya característica es diferente de dos. En otras palabras, se está trabajando en un campo en el que $1+1\ne 0$. Siempre que se mencionan las raíces de $P(x)$, pertenecen a alguna extensión $K$ de $k$ tal que $P(x)$ se factoriza en factores lineales en $K[x]$. Si $k$ es el conjunto $Q$ de números racionales, entonces $K$ puede ser el conjunto de números complejos o el de los números reales.

En algunos casos, el concepto de cúbica resolvente se define solo cuando $P(x)$ es una ecuación cuártica en forma reducida, es decir, cuando $a_1=0$.

Téngase en cuenta que las definiciones cuarta y quinta que figuran a continuación también tienen sentido y que la relación entre estas cúbicas resolventes y $P(x)$ sigue siendo válida si la característica de $k$ es igual a dos.

Primera definición

Supóngase que $P(x)$ es una ecuación cuártica reducida, es decir, que $a_1=0$. Una posible definición de la cúbica resolvente de $P(x)$ es:

$R_1(y)=8y^3+8a_2{y}^2+(2{a_2}^2-8a_4)y-{a_3}^2.$

El origen de esta definición radica en aplicar el método de Ferrari para encontrar las raíces de $P(x)$. Para ser más precisos:

$\begin{array}{cc}P(x)=0& ⟺x^4+a_2{x}^2=-a_{3}x-a_4\\ & ⟺{(x^2+\frac{a_2}{2})}^2=-a_{3}x-a_4+\frac{{a_2}^2}{4}.\end{array}$

Agregando una nueva incógnita $y$ a $x^2+\frac{a_2}{2}$, se obtiene:

$\begin{array}{cc}{(x^2+\frac{a_2}{2}+y)}^2& =-a_{3}x-a_4+\frac{{a_2}^2}{4}+2x^{2}y+a_{2}y+y^2\\ & =2y{x}^2-a_{3}x-a_4+\frac{{a_2}^2}{4}+a_{2}y+y^2.\end{array}$

Si esta expresión es un cuadrado, solo puede ser el cuadrado de

$\sqrt{2y}x-\frac{a_3}{2\sqrt{2y}}.$

Pero la igualdad

${(\sqrt{2y}x-\frac{a_3}{2\sqrt{2y}})}^2=2y{x}^2-a_{3}x-a_4+\frac{{a_2}^2}{4}+a_{2}y+y^2$

es equivalente a

$\frac{{a_3}^2}{8y}=-a_4+\frac{{a_2}^2}{4}+a_{2}y+y^2\text{,}$

y esto es lo mismo que la afirmación de que $R_1(y)=0$.

Si $y_0$ es una raíz de $R_1(y)$, entonces es una consecuencia de los cálculos realizados anteriormente para concluir que las raíces de $P(x)$ son las raíces del polinomio

$x^2-\sqrt{2y_0}x+\frac{a_2}{2}+y_0+\frac{a_3}{2\sqrt{2y_0}}$

junto con las raíces del polinomio

$x^2+\sqrt{2y_0}x+\frac{a_2}{2}+y_0-\frac{a_3}{2\sqrt{2y_0}}.$

Por supuesto, esto no tiene sentido si $y_0=0$, pero dado que el término constante de $R_1(y)$ es $a_4$, entonces $y_0$ es una raíz de $R_1(y)$ si y solo si $a_1=0$, y en este caso las raíces de $P(x)$ se pueden encontrar usando la fórmula cuadrática.

Segunda definición

Otra posible definición (todavía suponiendo que $P(x)$ es una ecuación cuártica reducida) es

$R_2(y)=8y^3-4a_2{y}^2-8a_{4}y+4a_2{a}_4-{a_3}^2$

El origen de esta definición es similar a la anterior. Esta vez, se comienza haciendo:

$\begin{array}{cc}P(x)=0& ⟺x^4=-a_2{x}^2-a_{3}x-a_4\\ & ⟺(x^2+y{)}^2=-a_2{x}^2-a_{3}x-a_4+2y{x}^2+y^2\end{array}$

y un cálculo similar al anterior muestra que esta última expresión es un cuadrado si y solo si

$8y^3-4a_2{y}^2-8a_{3}y+4a_2{a}_4-{a_3}^2=0\text{.}$

Un cálculo simple muestra que

$R_2(y+\frac{a_2}{2})=R_1(y).$

Tercera definición

Otra posible definición (nuevamente, suponiendo que $P(x)$ es una ecuación cuártica reducida) es

$R_3(y)=y^3+2a_2{y}^2+({a_2}^2-4a_4)y-{a_3}^2\text{.}$

El origen de esta definición radica en otro método para resolver ecuaciones cuárticas, a saber, el método de Descartes. Si se intenta encontrar las raíces de $P(x)$ expresándolas como producto de dos polinomios mónicos cuadráticos $x^2+\alpha x+\beta =0$ y $x^2-\alpha x+\gamma =0$, entonces

$P(x)=(x^2+\alpha x+\beta )(x^2-\alpha x+\gamma )⟺\{\begin{array}{c}\beta +\gamma -{\alpha }^2=a_2\\ \alpha (\gamma -\beta )=a_3\\ \beta \gamma =a_4.\end{array}$

Si hay una solución de este sistema con $\alpha \ne 0$ (teniendo en cuenta que la solución del sistema es cierta si ${\alpha }^2\ne 0$), el sistema anterior es equivalente a

$\{\begin{array}{c}\beta +\gamma =a_2+{\alpha }^2\\ \gamma -\beta =\frac{a_3}{\alpha }\\ \beta \gamma =a_4.\end{array}$

Esto es una consecuencia de las dos primeras ecuaciones, entonces

$\beta =\frac{1}{2}(a_2+{\alpha }^2-\frac{a_3}{\alpha })$

y

$\gamma =\frac{1}{2}(a_2+{\alpha }^2+\frac{a_3}{\alpha }).$

Después de reemplazar, en la tercera ecuación, $\beta$ y $\gamma$ por estos valores se obtiene

${(a_2+{\alpha }^2)}^2-\frac{{a_3}^2}{{\alpha }^2}=4a_4\text{,}$

y esto es equivalente a la afirmación de que ${\alpha }^2$ es una raíz de $R_3(y)$. Entonces, nuevamente, conocer las raíces de $R_3(y)$ ayuda a determinar las raíces de $P(x)$.

Téngase en cuenta que

$R_3(y)=R_1\left(\frac{y}{2}\right)\text{.}$

Cuarta definición

Aún es posible otra definición

$R_4(y)=y^3-a_2{y}^2+(a_1{a}_3-4a_4)y+(4a_2{a}_4-{a_1}^2{a}_4-{a_3}^2)$

De hecho, si las raíces de $P(x)$ son ${\alpha }_1,{\alpha }_2,{\alpha }_3$ y ${\alpha }_4$, entonces

$R_4(y)=(y-({\alpha }_1{\alpha }_2+{\alpha }_3{\alpha }_4))(y-({\alpha }_1{\alpha }_3+{\alpha }_2{\alpha }_4))(y-({\alpha }_1{\alpha }_4+{\alpha }_2{\alpha }_3))\text{,}$

Es un hecho deducido de las relaciones de Cardano-Vieta. En otras palabras, $R_4(y)$ es el polinomio mónico cuyas raíces son ${\alpha }_1{\alpha }_2+{\alpha }_3{\alpha }_4$, ${\alpha }_1{\alpha }_3+{\alpha }_2{\alpha }_4$ y ${\alpha }_1{\alpha }_4+{\alpha }_2{\alpha }_3$.

Es fácil ver esto, dado que

${\alpha }_1{\alpha }_2+{\alpha }_3{\alpha }_4-({\alpha }_1{\alpha }_3+{\alpha }_2{\alpha }_4)=({\alpha }_1-{\alpha }_4)({\alpha }_2-{\alpha }_3)\text{,}$

${\alpha }_1{\alpha }_3+{\alpha }_2{\alpha }_4-({\alpha }_1{\alpha }_4+{\alpha }_2{\alpha }_3)=({\alpha }_1-{\alpha }_2)({\alpha }_3-{\alpha }_4)\text{,}$

${\alpha }_1{\alpha }_2+{\alpha }_3{\alpha }_4-({\alpha }_1{\alpha }_4+{\alpha }_2{\alpha }_3)=({\alpha }_1-{\alpha }_3)({\alpha }_2-{\alpha }_4)\text{.}$

Por lo tanto, $P(x)$ tiene una raíz múltiple si y solo si $R_4(y)$ tiene una raíz múltiple. Más precisamente, $P(x)$ y $R_4(y)$ tienen el mismo discriminante.

Se debe tener en cuenta que si $P(x)$ es un polinomio reducido, entonces

$\begin{array}{cc}{R}_4(y)& =y^3-a_2{y}^2-4a_{4}y+(4a_2{a}_4-{a_3}^2)\\ & =R_2\left(\frac{y}{2}\right)\end{array}$

Quinta definición

Otra definición más es

$R_5(y)=y^3-2a_2{y}^2+({a_2}^2+a_1{a}_3-4a_4)y+{a_3}^2-a_1{a}_2{a}_3+{a_1}^2{a}_4\text{.}$

Si las raíces de $P(x)$ son ${\alpha }_1,{\alpha }_2,{\alpha }_3$ y ${\alpha }_4$, entonces:

$R_5(y)=(y-({\alpha }_1+{\alpha }_2)({\alpha }_3+{\alpha }_4))(y-({\alpha }_1+{\alpha }_3)({\alpha }_2+{\alpha }_4))(y-({\alpha }_1+{\alpha }_4)({\alpha }_2+{\alpha }_3))\text{,}$

nuevamente como consecuencia de las relaciones de Cardano-Vieta. En otras palabras, $R_5(y)$ es el polinomio mónico cuyas raíces son $({\alpha }_1+{\alpha }_2)({\alpha }_3+{\alpha }_4)$, $({\alpha }_1+{\alpha }_3)({\alpha }_2+{\alpha }_4)$ y $({\alpha }_1+{\alpha }_4)({\alpha }_2+{\alpha }_3)$.

Es fácil ver esto, pues

$({\alpha }_1+{\alpha }_2)({\alpha }_3+{\alpha }_4)-({\alpha }_1+{\alpha }_3)({\alpha }_2+{\alpha }_4)=-({\alpha }_1-{\alpha }_4)({\alpha }_2-{\alpha }_3)\text{,}$

$({\alpha }_1+{\alpha }_2)({\alpha }_3+{\alpha }_4)-({\alpha }_1+{\alpha }_4)({\alpha }_2+{\alpha }_3)=-({\alpha }_1-{\alpha }_3)({\alpha }_2-{\alpha }_4)\text{,}$

$({\alpha }_1+{\alpha }_3)({\alpha }_2+{\alpha }_4)-({\alpha }_1+{\alpha }_4)({\alpha }_2+{\alpha }_3)=-({\alpha }_1-{\alpha }_2)({\alpha }_3-{\alpha }_4)\text{.}$

Por lo tanto, como sucede con $R_4(y)$, $P(x)$ tiene una raíz múltiple si y solo si $R_5(y)$ tiene una raíz múltiple. Más precisamente, $P(x)$ y $R_5(y)$ tienen el mismo discriminante. Esto también es una consecuencia del hecho de que $R_5(y+a_2)=R_4(y)$.

Téngase en cuenta que si $P(x)$ es un polinomio cuártico reducido, entonces:

$\begin{array}{cc}{R}_5(y)& =y^3-2a_2{y}^2+({a_2}^2-4a_4)y+{a_3}^2\\ & =-R_3(-y)\\ & =-R_1(-\frac{y}{2})\text{.}\end{array}$

Aplicaciones

Resolución de ecuaciones cuárticas

Se explicó anteriormente cómo pueden usarse $R_1(y)$, $R_2(y)$ y $R_3(y)$ para encontrar las raíces de $P(x)$ si este polinomio está reducido. En el caso general, simplemente se tienen que encontrar las raíces del polinomio reducido $P(x-\frac{a_1}{4})$. Para cada raíz $x_0$ de este polinomio, $x_0-\frac{a_1}{4}$ es una raíz de $P(x)$.

Factorización de polinomios cuárticos

Si un polinomio cuártico $P(x)$ es reducible en $k[x]$, entonces es el producto de dos polinomios cuadráticos o el producto de un polinomio lineal por un polinomio cúbico. Esta segunda posibilidad ocurre si y solo si $P(x)$ tiene una raíz en $k$. Para determinar si $P(x)$ puede expresarse o no como el producto de dos polinomios cuadráticos, suponiendo, por simplicidad, que $P(x)$ es un polinomio reducido. Como se vio anteriormente, si la cúbica resolvente $R_3(y)$ tiene una raíz no nula de la forma ${\alpha }^2$ para algunos $\alpha \in k$, entonces existe tal descomposición polinómica.

Esto puede usarse para demostrar que, en $R(x)$, cada polinomio cuártico sin raíces reales puede expresarse como el producto de dos polinomios cuadráticos. Sea $P(x)$ tal polinomio, se puede suponer sin pérdida de generalidad que $P(x)$ es un polinomio mónico. También se puede suponer sin pérdida de generalidad que es un polinomio reducido, porque $P(x)$ puede expresarse como el producto de dos polinomios cuadráticos si y solo si $P(x-\frac{a_1}{4})$ puede hacerlo y este polinomio es uno reducido. Entonces $R_3(y)=y^3+2a_2{y}^2+({a_2}^2-4a_4)y-{a_3}^2$. Hay dos casos:

• Si $a_3\ne 0$ entonces $R_3(0)=-{a_3}^2>0$. Dado que $R_3(y)>0$ si $y$ es lo suficientemente grande, entonces, según el teorema del valor intermedio, $R_3(y)$ tiene una raíz $y_0$ con $y_0>0$. Entonces, se puede tomar $\alpha =\sqrt{y_0}$.
• Si $a_3=0$, entonces $R_3(y)=y^3+2a_2{y}^2+({a_2}^2-4a_4)y$. Las raíces de este polinomio son cero y las raíces del polinomio cuadrático $y^2+2a_{2}y+({a_2}^2-4a_4)$. Si ${a_2}^2-4a_4<0$, entonces el producto de las dos raíces de este polinomio es menor que Plantilla:Math y por lo tanto tiene una raíz mayor que cero (que resulta ser $-a_2+\sqrt{a_4}$) y se puede tomar $\alpha$ como la raíz cuadrada de esa raíz. De lo contrario, ${a_2}^2-4a_4\ge 0$, y entonces

$P(x)=(x^2+\frac{a_2+\sqrt{{a_2}^2-4a_4}}{2})(x^2+\frac{a_2-\sqrt{{a_2}^2-4a_4}}{2})\text{.}$

En términos más generales, si $k$ es un cuerpo cerrado real, entonces cada polinomio cuártico sin raíces en $k$ puede expresarse como el producto de dos polinomios cuadráticos en $k[x]$. De hecho, esta declaración puede expresarse en lógica de primer orden y cualquier declaración que se mantenga para $R(x)$ también se cumple para cualquier campo cerrado real.

Se puede usar un enfoque similar para obtener un algoritmo para determinar si un polinomio cuártico $P(x)\in Q(x)$ es reducible y, si es así, cómo expresarlo como un producto de polinomios de menor grado. Nuevamente, supondremos que $P(x)$ es mónico y reducido. Entonces $P(x)$ es reducible si y solo si se cumple al menos una de las siguientes condiciones:

• El polinomio $P(x)$ tiene una raíz racional (esto se puede determinar utilizando el teorema de la raíz racional).
• La cúbica resolvente $R_3(y)$ tiene una raíz de la forma ${\alpha }^2$, para algún número racional no nulo $\alpha$ (de nuevo, esto se puede determinar utilizando el teorema de la raíz racional).
• El número ${a_2}^2-4a_4$ es el cuadrado de un número racional, y además $a_3=0$.

En efecto:

• Si $P(x)$ tiene una raíz racional $r$, entonces $P(x)$ es el producto de $x-r$ por un polinomio cúbico en $Q[x]$, que puede determinarse por división polinómica o por la regla de Ruffini.
• Si hay un número racional $\alpha \ne 0$ tal que ${\alpha }^2$ es una raíz de $R_3(y)$, ya se mostró anteriormente cómo expresar $P(x)$ como producto de dos polinomios cuadráticos en $Q[x]$.
• Finalmente, si se cumple la tercera condición y si $\delta \in Q$ es tal que ${\delta }^2={a_2}^2-4a_4$, entonces $P(x)=(x^2+\frac{a_2+\delta }{2})(x^2+\frac{a_2-\delta }{2})$.

Grupos de Galois de polinomios cuárticos irreducibles

La cúbica resolvente de un polinomio cuártico irreducible $P(x)$ puede usarse para determinar su grupo de Galois Plantilla:Math; es decir, el grupo de Galois del campo de división de $P(x)$. Sea $n$ el grado sobre $k$ del campo de división de la cúbica resolvente (puede ser $R_4(y)$ o $R_5(y)$; tienen el mismo campo de división). Entonces, el grupo $G$ es un subgrupo del grupo simétrico $S_4$. Más precisamente:

• Si $n=1$ (es decir, si los factores cúbicos resolventes en factores lineales en $k$), entonces Plantilla:Mvar es el grupo Plantilla:Math}.
• Si $n=2$ (es decir, si la cúbica resolvente tiene una y, salvo multiplicidad, solo una raíz en $k$), entonces, para determinar $G$, se puede determinar si $P(x)$ sigue siendo irreducible después de unir al campo $k$ las raíces de la cúbica resolvente. De lo contrario, entonces $G$ es un grupo cíclico de cuarto orden; más precisamente, es uno de los tres subgrupos cíclicos de $S_4$ generado por cualquiera de sus seis ciclos cuádruples. Si aún es irreducible, entonces $G$ es uno de los tres subgrupos de $S_4$ de octavo orden, cada uno de los cuales es isomorfo al grupo diédrico de octavo orden.
• Si $n=3$, entonces $G$ es el grupo alternante $A_4$.
• Si $n=6$, entonces $G$ es todo el grupo $S_4$.

Véase también

• Teoría de Galois