N-esfera

Vista alámbrica de una 2-esfera como un operador de proyección

Así como una proyección estereográfica puede representar la superficie de una esfera en un plano, también se puede proyectar una 3-esfera en el espacio tridimensional. Esta imagen muestra las tres direcciones de coordenadas proyectadas en el espacio tridimensional: paralelos (rojo), meridianos (azul) e hipermeridianos (verde). Debido a la propiedad de conformidad de la proyección estereográfica, las curvas se cruzan entre sí ortogonalmente (en los puntos amarillos) al igual que en 4D. Todas las curvas son circunferencias: las curvas que intersecan Plantilla:Angbr tienen un radio infinito (se proyectan como líneas rectas)

En matemáticas, una n-esfera (o hiperesfera) es la generalización de la «esfera» a un espacio euclídeo de dimensión arbitraria. En otras palabras, la n-esfera es una hipersuperficie del espacio euclídeo ${ℝ}^{n+1}$, denotada en general como ${𝕊}^n$. Constituye uno de los ejemplos más sencillos de variedad matemática.

Desde un punto de vista analítico, una Plantilla:Math-esfera es un espacio topológico que es homeomorfo a una Plantilla:Math-esfera estándar, que es el conjunto de puntos en un espacio euclídeo Plantilla:Math-dimensional que se encuentran a una distancia constante Plantilla:Mvar respecto a un punto fijo, llamado centro. Cuando la esfera tiene un radio unidad, es habitual llamarla Plantilla:Math-esfera unidad, o simplemente Plantilla:Math-esfera por brevedad. En términos de la norma estándar, una Plantilla:Math-esfera se define como

$S^n=\{x\in {ℝ}^{n+1}:\Vert x\Vert =1\},$

y una Plantilla:Math-esfera de radio Plantilla:Mvar se puede definir como

$S^n(r)=\{x\in {ℝ}^{n+1}:\Vert x\Vert =r\}.$

La 0-esfera es un par de puntos sobre una recta a una unidad de distancia del origen, la 1-esfera es una circunferencia en el plano y la 2-esfera es una esfera ordinaria dentro del espacio tridimensional.

La dimensión de una Plantilla:Math-esfera es Plantilla:Mvar, y no debe confundirse con la dimensión Plantilla:Math del espacio euclídeo en el que queda naturalmente embebida. Una Plantilla:Math-esfera es la superficie o límite de una bola Plantilla:Math dimensional.

En particular:

• El par de puntos en los extremos de un segmento (unidimensional) es una 0-esfera
• Un circunferencia, que es el contorno unidimensional de un círculo (bidimensional), es una Plantilla:Nowrap
• La superficie bidimensional de una bola (tridimensional) en un espacio tridimensional es una Plantilla:Nowrap, a menudo simplemente llamada esfera
• La frontera tridimensional de una 4-bola (cuatro dimensiones) en el espacio euclídeo tetradimensional, es un 3-esfera, también conocida como glomo
• El límite Plantilla:Math-dimensional de una Plantilla:Mvar-bola (Plantilla:Mvar-dimensional) es una Plantilla:Nowrap.

Para Plantilla:Math, las Plantilla:Math-esferas que son variedades diferenciables pueden caracterizarse (hasta un difeomorfismo) como variedades Plantilla:Math-dimensionales conexas de curvatura constante y positiva. Las Plantilla:Math-esferas admiten varias otras descripciones topológicas: por ejemplo, se pueden construir pegando dos espacios euclídeos Plantilla:Math-dimensionales, identificando el límite de un [[Hipercubo|Plantilla:Math-cubo]] con un punto, o (inductivamente) formando la suspensión de una Plantilla:Math-esfera. La 1-esfera es la 1-variedad que es una circunferencia, que no es simplemente conexa. La 0-esfera es la 0-variedad que consta de dos puntos, que ni siquiera es conexa.

Definición

Dado un espacio euclídeo E de dimensión n+1, A un punto de E, y R un número real estrictamente positivo, se le llama hiperesfera de centro A y radio R al conjunto de puntos M tales que su distancia a A vale exactamente R.

La n+1-tupla de puntos (x₁,x₂,…,x_n+1) que están en una n-esfera (Sⁿ) se representa con la ecuación:

donde el centro es el origen de coordenadas O (0,0,...,0). Teniendo como datos un punto fijo $P=(p_1,p_2,\dots ,p_n)$ llamado centro y el radio R, real positivo, siendo $X=(x_1,x_2,\dots ,x_n)$ un punto cualquiera de la hiperesfera, la ecuación correspondiente es,

o escrito en forma vectorial, como:

Descripción

Para cualquier número natural Plantilla:Math, una Plantilla:Math-esfera de radio Plantilla:Math se define como el conjunto de puntos en el espacio euclídeo Plantilla:Math-dimensional que están a una distancia Plantilla:Math de un punto fijo Plantilla:Math, donde Plantilla:Math puede ser cualquier número real positivo y donde Plantilla:Math puede ser cualquier punto en el espacio Plantilla:Math dimensional. En particular:

• Una 0-esfera es un par de puntos Plantilla:Math, y es el límite de un segmento recto (1-bola)
• Una 1-esfera es una circunferencia de radio Plantilla:Math centrada en Plantilla:Math, y es el límite de un disco (2-bola)
• Una 2-esfera es un esfera bidimensional ordinaria en un espacio euclídeo tridimensional, y es el límite de una bola ordinaria Plantilla:Nowrap
• Una 3-esfera es una esfera tridimensional en un espacio euclídeo de 4 dimensiones

Coordenadas euclídeas en el Plantilla:Math-espacio

El conjunto de puntos en el espacio Plantilla:Math, Plantilla:Math, que definen una Plantilla:Math-esfera, $S^n(r)$, está representado por la ecuación:

$r^2=\sum _{i=1}^{n+1}{(x_i-c_i)}^2$

donde Plantilla:Math = Plantilla:Math es un punto central y Plantilla:Math es el radio.

La Plantilla:Math-esfera anterior existe en el espacio euclídeo Plantilla:Math-dimensional y es un ejemplo de Plantilla:Math-variedad. La forma de volumen Plantilla:Math de una Plantilla:Math-esfera de radio Plantilla:Math viene dada por

$\omega =\frac{1}{r}\sum _{j=1}^{n+1}(-1{)}^{j-1}{x}_{j}d{x}_1\wedge \cdots \wedge d{x}_{j-1}\wedge d{x}_{j+1}\wedge \cdots \wedge d{x}_{n+1}=*dr$

donde Plantilla:Math es el dual de Hodge; véase Plantilla:Harvtxt para una discusión y prueba de esta fórmula en el caso Plantilla:Math. Como resultado,

$dr\wedge \omega =d{x}_1\wedge \cdots \wedge d{x}_{n+1}.$

Plantilla:Math-bola

El espacio encerrado por una Plantilla:Math-esfera se llama Plantilla:Math-bola. Una Plantilla:Math-bola es cerrada si incluye la Plantilla:Math-esfera, y es abierta si no incluye la Plantilla:Math-esfera.

Específicamente:

• Una 1-bola, un segmento, es el interior de una 0-esfera
• Una 2-bola, un círculo, es el interior de una circunferencia (1-esfera)
• Una 3-bola, una bola ordinaria, es el interior de una esfera (2-esfera)
• Una 4-bola es el interior de una 3-esfera, y así sucesivamente

Descripción topológica

Topológicamente, una Plantilla:Math-esfera se puede construir como una compactación en un punto del espacio euclídeo Plantilla:Math-dimensional. Brevemente, la Plantilla:Math-esfera puede describirse como Plantilla:Math, que es un espacio euclídeo Plantilla:Math-dimensional más un único punto que representa el infinito en todas las direcciones. En particular, si se elimina un único punto de una Plantilla:Math-esfera, se convierte en homeomórfica a Plantilla:Math. Esta circunstancia sustenta la base de la proyección estereográfica.

Volumen y área de la superficie

Plantilla:Math y Plantilla:Math son el volumen Plantilla:Math-dimensional de una [[Bola (matemática)|Plantilla:Math-bola]] y el área de la superficie de la Plantilla:Math-esfera incrustada en la dimensión Plantilla:Math, respectivamente, ambas de radio Plantilla:Math.

Las constantes Plantilla:Math y Plantilla:Math (para Plantilla:Math, la bola unitaria y la esfera) están relacionadas por las recurrencias:

$\begin{array}{cccc}{V}_0& =1& V_{n+1}& =\frac{S_n}{n+1}\\ S_0& =2& S_{n+1}& =2\pi V_n\end{array}$

Las superficies y los volúmenes también se pueden dar en forma cerrada:

$\begin{array}{cc}{S}_n(R)& =\frac{2{\pi }^{n/2}}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}{R}^{n-1}\\ V_n(R)& =\frac{{\pi }^{\frac{n}{2}}}{\mathrm{\Gamma }(\frac{n}{2}+1)}{R}^n\end{array}$

donde Plantilla:Math es la función gamma. Las deducciones de estas ecuaciones se dan en esta sección.

Gráficos de volúmenes (V) y de áreas de la superficie (S) de n-bolas de radio 1. Desplazar el cursor en el archivo SVG sobre un punto para resaltarlo y obtener su valor

En general, el volumen de la Plantilla:Math-bola en el espacio euclídeo Plantilla:Math y el área de la superficie de la Plantilla:Math-esfera en el espacio euclídeo Plantilla:Math-dimensional, de radio Plantilla:Math, son proporcionales a la potencia Plantilla:Math del radio Plantilla:Math (con diferentes constantes de proporcionalidad que varían con Plantilla:Math). Se escribe Plantilla:Math para el volumen de la Plantilla:Math-bola y Plantilla:Math para el área de la superficie de la Plantilla:Math-esfera, ambas de radio Plantilla:Math, donde Plantilla:Math y Plantilla:Math son los valores para el caso del radio unidad.

En teoría, se podrían comparar los valores de Plantilla:Math y Plantilla:Math para Plantilla:Math. Sin embargo, esto es algo sin sentido. Por ejemplo, si Plantilla:Math y Plantilla:Math, es como comparar un número de metros cuadrados con un número diferente de metros cúbicos. La misma falta de sentido se aplica a una comparación de Plantilla:Math y Plantilla:Math para Plantilla:Math.

Fórmula del volumen

El volumen del espacio delimitado por una hiperesfera de dimensión n-1 y de radio R, que es una bola euclídea de dimensión n viene determinado por:

donde $\mathrm{\Gamma }$ es la función gamma.

Nótese la particularidad de que $V_n$ se incrementa desde n=1 hasta un máximo y luego comienza a disminuir y tiende a cero cuando n tiende a infinito. En el caso de que R=1 el volumen máximo se obtiene cuando n=5.

Por ejemplo, el volumen de una hiperfesfera de radio R en el espacio cuadridimensional aplicando la fórmula Plantilla:Eqnref para n=4 resulta

Ejemplos

La 0-bola consiste en un solo punto. La medida de Hausdorff en 0 dimensiones es el número de puntos en un conjunto. Entonces,

$V_0=1.$

La 1-bola unidad es el intervalo Plantilla:Math de longitud 2. Entonces,

$V_1=2.$

La 0-esfera consiste en sus dos puntos finales, Plantilla:Math. Entonces,

$S_0=2.$

La 1-esfera unidad es la circunferencia unidad en el plano euclídeo, cuyo perímetro (medida unidimensional) mide

$S_1=2\pi .$

La región encerrada por la 1-esfera unidad es la 2-bola o disco unidad, que tiene un área (medida bidimensional) de

$V_2=\pi .$

Análogamente, en el espacio euclídeo tridimensional, el área de la superficie (medida bidimensional) de la 2-esfera unidad está dada por

$S_2=4\pi .$

y el volumen incluido es la capacidad (medida tridimensional) de la 3-bola unidad, dada por

$V_3=\frac{4}{3}\pi .$

Recurrencias

El área de la superficie, o más adecuadamente, el volumen Plantilla:Math-dimensional, de la Plantilla:Math-esfera en el límite de la Plantilla:Math-bola de radio Plantilla:Math está relacionado con el volumen de la bola por la ecuación diferencial

$S_n{R}^n=\frac{d{V}_{n+1}{R}^{n+1}}{dR}=(n+1)V_{n+1}{R}^n,$

o, de manera equivalente, representando la Plantilla:Math-bola unidad como la unión de Plantilla:Math-esferas concéntricas anidadas en forma de corona esférica,

$V_{n+1}=\underset{0}{\overset{1}{\int }}{S}_n{r}^{n}dr.$

Entonces,

$V_{n+1}=\frac{S_n}{n+1}.$

También se puede representar la Plantilla:Math-esfera unidad como la unión de toros, cada uno el producto de un círculo (1-esfera) con una Plantilla:Math-esfera. Siendo Plantilla:Math y Plantilla:Math, de modo que Plantilla:Math y Plantilla:Math, entonces:

$\begin{array}{cc}{S}_{n+2}& =\underset{0}{\overset{\frac{\pi }{2}}{\int }}{S}_{1}r\cdot S_n{R}^{n}d\theta \\ & =\underset{0}{\overset{\frac{\pi }{2}}{\int }}{S}_1\cdot S_n{R}^n\cos \theta d\theta \\ & =\underset{0}{\overset{1}{\int }}{S}_1\cdot S_n{R}^{n}dR\\ & =S_1\underset{0}{\overset{1}{\int }}{S}_n{R}^{n}dR\\ & =2\pi V_{n+1}.\end{array}$

Desde Plantilla:Math, la ecuación

$S_{n+1}=2\pi V_n$

se cumple para todos los Plantilla:Math.

Esto completa la deducción de las recurrencias:

$\begin{array}{cccc}{V}_0& =1& V_{n+1}& =\frac{S_n}{n+1}\\ S_0& =2& S_{n+1}& =2\pi V_n\end{array}$

Formas cerradas

Combinando las recurrencias, se puede ver que

$V_{n+2}=2\pi \frac{V_n}{n+2}.$

Entonces, es simple mostrar por inducción que para k,

$\begin{array}{cc}{V}_{2k}& =\frac{{\left(2\pi \right)}^k}{(2k)!!}=\frac{{\pi }^k}{k!}\\ V_{2k+1}& =\frac{2{\left(2\pi \right)}^k}{(2k+1)!!}=\frac{2k!{\left(4\pi \right)}^k}{(2k+1)!}\end{array}$

donde Plantilla:Math denota el doble factorial, definido para números naturales impares Plantilla:Math por Plantilla:Math y de manera similar para números pares Plantilla:Math.

En general, el volumen en el espacio euclídeo Plantilla:Math-dimensional de la Plantilla:Math-bola unidad viene dado por

$V_n=\frac{{\pi }^{\frac{n}{2}}}{\mathrm{\Gamma }(\frac{n}{2}+1)}$

donde Plantilla:Math es la función gamma, que satisface Plantilla:Math, Plantilla:Math y Plantilla:Math.

Multiplicando Plantilla:Math por Plantilla:Math, diferenciando con respecto a Plantilla:Math, y luego configurando Plantilla:Math, se obtiene la forma cerrada

$S_{n-1}=\frac{n{\pi }^{\frac{n}{2}}}{\mathrm{\Gamma }(\frac{n}{2}+1)}.$

Otras relaciones

En la imagen, Plantilla:Math se refiere a la dimensión del espacio euclídeo de contorno, que también es la dimensión intrínseca del sólido cuyo volumen se enumera, pero que es 1 más que la dimensión intrínseca de la esfera cuya área de la superficie se indica.

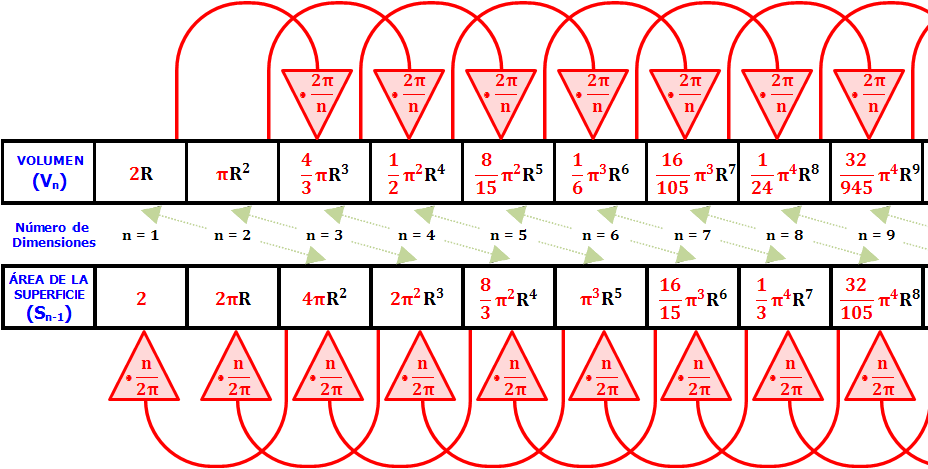
Las flechas rojas curvas muestran la relación entre diferentes fórmulas: la fórmula a la que apunta la flecha, se obtiene multiplicando la fórmula de la cola por el factor que figura en la punta de la flecha (donde Plantilla:Math se toma el valor asociado a la celda a la que se señala).

Si se quisiera invertir el sentido de las flechas de abajo, se debería tomar la fórmula a la que señala la flecha, y multiplicarla por Plantilla:Math, siendo n la de la celda de mayor grado.

Por otro lado, el área de la superficie Plantilla:Math de la esfera en Plantilla:Math dimensiones, es exactamente Plantilla:Math veces el volumen Plantilla:Math contenido por la esfera en Plantilla:Math dimensiones (flechas de color verde claro)

Las recurrencias se pueden combinar para dar una relación de recurrencia de "dirección inversa" para el área de la superficie, como se muestra en el diagrama:

$S_{n-1}=\frac{n}{2\pi }{S}_{n+1}$

El cambio del índice Plantilla:Math a Plantilla:Math produce las relaciones de recurrencia siguientes:

$\begin{array}{cc}{V}_n& =\frac{2\pi }{n}{V}_{n-2}\\ S_{n-1}& =\frac{2\pi }{n-2}{S}_{n-3}\end{array}$

donde Plantilla:Math, Plantilla:Math, Plantilla:Math y Plantilla:Math.

La relación de recurrencia para Plantilla:Math también se puede probar a través de la integración con coordenadas polares bidimensionales:

$\begin{array}{cc}{V}_n& =\underset{0}{\overset{1}{\int }}\underset{0}{\overset{2\pi }{\int }}{V}_{n-2}{\left(\sqrt{1-r^2}\right)}^{n-2}rd\theta dr\\ & =\underset{0}{\overset{1}{\int }}\underset{0}{\overset{2\pi }{\int }}{V}_{n-2}{(1-r^2)}^{\frac{n}{2}-1}rd\theta dr\\ & =2\pi V_{n-2}\underset{0}{\overset{1}{\int }}{(1-r^2)}^{\frac{n}{2}-1}rdr\\ & =2\pi V_{n-2}{[-\frac{1}{n}{(1-r^2)}^{\frac{n}{2}}]}_{r=0}^{r=1}\\ & =2\pi V_{n-2}\frac{1}{n}=\frac{2\pi }{n}{V}_{n-2}.\end{array}$

Coordenadas esféricas

Se puede definir un sistema de coordenadas en un espacio euclídeo Plantilla:Math-dimensional que es análogo al sistema de coordenadas esféricas definido para el espacio euclídeo tridimensional, en el que las coordenadas consisten en una coordenada radial Plantilla:Math, y las coordenadas angulares Plantilla:Math Plantilla:Math, donde los ángulos Plantilla:Math se extienden sobre Plantilla:Math radianes (o entre Plantilla:Math grados) y Plantilla:Math varía sobre Plantilla:Math radianes (o entre Plantilla:Math grados). Si Plantilla:Math son las coordenadas cartesianas, entonces se puede calcular Plantilla:Math a partir de Plantilla:Math con:

$\begin{array}{cc}{x}_1& =r\cos ({\phi }_1)\\ x_2& =r\mathrm{sen}({\phi }_1)\cos ({\phi }_2)\\ x_3& =r\mathrm{sen}({\phi }_1)\mathrm{sen}({\phi }_2)\cos ({\phi }_3)\\ & ⋮\\ x_{n-1}& =r\mathrm{sen}({\phi }_1)\cdots \mathrm{sen}({\phi }_{n-2})\cos ({\phi }_{n-1})\\ x_n& =r\mathrm{sen}({\phi }_1)\cdots \mathrm{sen}({\phi }_{n-2})\mathrm{sen}({\phi }_{n-1}).\end{array}$

Excepto en los casos especiales descritos a continuación, la transformación inversa es única:

$\begin{array}{cc}r& =\sqrt{{x_n}^2+{x_{n-1}}^2+\cdots +{x_2}^2+{x_1}^2}\\ {\phi }_1& =\mathrm{arccot}\frac{x_1}{\sqrt{{x_n}^2+{x_{n-1}}^2+\cdots +{x_2}^2}}& & =\arccos \frac{x_1}{\sqrt{{x_n}^2+{x_{n-1}}^2+\cdots +{x_1}^2}}\\ {\phi }_2& =\mathrm{arccot}\frac{x_2}{\sqrt{{x_n}^2+{x_{n-1}}^2+\cdots +{x_3}^2}}& & =\arccos \frac{x_2}{\sqrt{{x_n}^2+{x_{n-1}}^2+\cdots +{x_2}^2}}\\ & ⋮& & ⋮\\ {\phi }_{n-2}& =\mathrm{arccot}\frac{x_{n-2}}{\sqrt{{x_n}^2+{x_{n-1}}^2}}& & =\arccos \frac{x_{n-2}}{\sqrt{{x_n}^2+{x_{n-1}}^2+{x_{n-2}}^2}}\\ {\phi }_{n-1}& =2\mathrm{arccot}\frac{x_{n-1}+\sqrt{x_n^2+x_{n-1}^2}}{x_n}& & =\{\begin{array}{cc}\arccos \frac{x_{n-1}}{\sqrt{{x_n}^2+{x_{n-1}}^2}}& x_n\ge 0\\ 2\pi -\arccos \frac{x_{n-1}}{\sqrt{{x_n}^2+{x_{n-1}}^2}}& x_n<0\end{array}.\end{array}$

donde si Plantilla:Math para algunos Plantilla:Math pero todos Plantilla:Math son cero, entonces Plantilla:Math cuando Plantilla:Math y Plantilla:Math (180 grados) cuando Plantilla:Math.

Hay algunos casos especiales donde la transformación inversa no es única; Plantilla:Math para cualquier Plantilla:Math será ambiguo siempre que todos los Plantilla:Math sean cero; en este caso, Plantilla:Math puede elegirse como cero.

Volumen esférico y elementos de área

Expresando las medidas angulares en radianes, el elemento volumen en el espacio euclídeo Plantilla:Math-dimensional se encontrará a partir del Jacobiano de la transformación:

$\left(\begin{array}{cccccc}\cos ({\phi }_1)& -r\mathrm{sen}({\phi }_1)& 0& 0& \cdots & 0\\ \mathrm{sen}({\phi }_1)\cos ({\phi }_2)& r\cos ({\phi }_1)\cos ({\phi }_2)& -r\mathrm{sen}({\phi }_1)\mathrm{sen}({\phi }_2)& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & & ⋮\\ & & & & & 0\\ \mathrm{sen}({\phi }_1)\cdots \mathrm{sen}({\phi }_{n-2})\cos ({\phi }_{n-1})& \cdots & \cdots & & & -r\mathrm{sen}({\phi }_1)\cdots \mathrm{sen}({\phi }_{n-2})\mathrm{sen}({\phi }_{n-1})\\ \mathrm{sen}({\phi }_1)\cdots \mathrm{sen}({\phi }_{n-2})\mathrm{sen}({\phi }_{n-1})& r\cos ({\phi }_1)\cdots \mathrm{sen}({\phi }_{n-1})& \cdots & & & r\mathrm{sen}({\phi }_1)\cdots \mathrm{sen}({\phi }_{n-2})\cos ({\phi }_{n-1})\end{array}\right)$

$\begin{array}{cc}{d}^{n}V& =|\det \frac{\partial (x_i)}{\partial (r,{\phi }_j)}|drd{\phi }_{1}d{\phi }_2\cdots d{\phi }_{n-1}\\ & =r^{n-1}{\mathrm{sen}}^{n-2}({\phi }_1){\mathrm{sen}}^{n-3}({\phi }_2)\cdots \mathrm{sen}({\phi }_{n-2})drd{\phi }_{1}d{\phi }_2\cdots d{\phi }_{n-1}\end{array}$

y la ecuación anterior para el volumen de la Plantilla:Math-bola se puede recuperar integrando:

$V_n=\underset{{\phi }_{n-1}=0}{\overset{2\pi }{\int }}\underset{{\phi }_{n-2}=0}{\overset{\pi }{\int }}\cdots \underset{{\phi }_1=0}{\overset{\pi }{\int }}\underset{r=0}{\overset{R}{\int }}{d}^{n}V.$

De manera similar, el elemento del área de superficie de la Plantilla:Math-esfera, que generaliza el elemento de área de la 2-esfera, viene dado por

$d_{S^{n-1}}V={\mathrm{sen}}^{n-2}({\phi }_1){\mathrm{sen}}^{n-3}({\phi }_2)\cdots \mathrm{sen}({\phi }_{n-2})d{\phi }_{1}d{\phi }_2\cdots d{\phi }_{n-1}.$

La elección natural de una base ortogonal sobre las coordenadas angulares es un producto de polinomios ultraesféricos,

$\begin{array}{cc}& \underset{0}{\overset{\pi }{\int }}{\mathrm{sen}}^{n-j-1}\left({\phi }_j\right)C_s^{\left(\frac{n-j-1}{2}\right)}\cos \left({\phi }_j\right)C_{s^{\prime }}^{\left(\frac{n-j-1}{2}\right)}\cos \left({\phi }_j\right)d{\phi }_j\\ & =\frac{2^{3-n+j}\pi \mathrm{\Gamma }(s+n-j-1)}{s!(2s+n-j-1){\mathrm{\Gamma }}^2\left(\frac{n-j-1}{2}\right)}{\delta }_{s,s^{\prime }}\end{array}$

para Plantilla:Math, y Plantilla:Math para el ángulo Plantilla:Math en concordancia con los armónicos esféricos.

Proyección estereográfica

Al igual que una esfera bidimensional incrustada en tres dimensiones se puede representar en un plano bidimensional mediante una proyección estereográfica, una Plantilla:Math-esfera se puede representar en un hiperplano Plantilla:Math-dimensional mediante la versión Plantilla:Math-dimensional de la proyección estereográfica. Por ejemplo, el punto Plantilla:Math en una esfera bidimensional de radio 1 se asigna al punto Plantilla:Math en el plano Plantilla:Math. En otras palabras,

$[x,y,z]\mapsto [\frac{x}{1-z},\frac{y}{1-z}].$

Del mismo modo, la proyección estereográfica de una Plantilla:Math-esfera Plantilla:Math de radio 1 se correlacionará con el hiperplano dimensional Plantilla:Math Plantilla:Math perpendicular al eje Plantilla:Math como

$[x_1,x_2,\dots ,x_n]\mapsto [\frac{x_1}{1-x_n},\frac{x_2}{1-x_n},\dots ,\frac{x_{n-1}}{1-x_n}].$

Generación de puntos aleatorios

Uniformemente al azar en una Plantilla:Math-esfera

Un conjunto de puntos distribuidos uniformemente en la superficie de una 2-esfera unidad generado usando el algoritmo de Marsaglia

Para generar puntos aleatorios distribuidos uniformemente en la Plantilla:Math-esfera unidad (es decir, la superficie de la Plantilla:Math-bola unidad),Plantilla:Harvtxt proporciona el siguiente algoritmo:

Genérese un vector Plantilla:Math-dimensional de distribución normal (es suficiente usar Plantilla:Math, aunque en realidad la elección de la varianza es arbitraria), Plantilla:Math. Ahora, calcúlese el radio de este punto:

$r=\sqrt{x_1^2+x_2^2+\cdots +x_n^2}.$

El vector Plantilla:Math se distribuye uniformemente sobre la superficie de la Plantilla:Math-bola unidad.

Una alternativa dada por Marsaglia es seleccionar uniformemente al azar un punto Plantilla:Math en el [[Hipercubo|Plantilla:Math-cubo]] unidad, muestreando cada Plantilla:Math independientemente de la distribución uniforme continua sobre Plantilla:Math, calculando Plantilla:Math como arriba, y rechazando el punto y remuestreando si Plantilla:Math (es decir, si el punto no está en la Plantilla:Math-bola), y cuando se obtiene un punto en la bola, se escala hacia la superficie esférica por el factor Plantilla:Math; de forma que de nuevo Plantilla:Math se distribuye uniformemente sobre la superficie de la Plantilla:Math-bola unidad.

Uniformemente al azar dentro de una Plantilla:Math-bola

Con un punto seleccionado al azar uniformemente desde la superficie de la Plantilla:Math-esfera unidad (por ejemplo, usando el algoritmo de Marsaglia), se necesita solo un radio para obtener un punto uniformente al azar desde dentro de la Plantilla:Math-bola unidad. Si Plantilla:Math es un número generado uniformemente al azar en el intervalo Plantilla:Math y Plantilla:Math es un punto seleccionado uniformemente al azar de la Plantilla:Math-esfera unidad, entonces Plantilla:Math se distribuye uniformemente dentro de la Plantilla:Math-bola unidad.

Alternativamente, los puntos se pueden muestrear uniformemente desde dentro de la Plantilla:Math-bola unidad mediante una reducción desde la Plantilla:Math-esfera unidad. En particular, si Plantilla:Math es un punto seleccionado uniformemente de la Plantilla:Math-esfera unidad, entonces Plantilla:Math se distribuye uniformemente dentro de la Plantilla:Math-bola unidad (es decir, simplemente descartando dos coordenadas).

Si Plantilla:Math es suficientemente grande, la mayor parte del volumen de la Plantilla:Math-bola estará contenido en la región muy cercana de su superficie, por lo que un punto seleccionado de ese volumen probablemente también estará cerca de la superficie. Este es uno de los fenómenos que conducen a la llamada maldición de la dimensión, que surge en algunas aplicaciones numéricas.

Esferas específicas

Proyección en 2D de una proyección en 3D de una hiperesfera 4D.

0-esfera

El par de puntos Plantilla:Math con topología discreta para Plantilla:Math. Se trata de la única esfera que no es un conjunto conexo. Posee una estructura de grupo de Lie natural; isomorfo a O (1). Paralelizable

1-esfera

También conocida como circunferencia. Posee un grupo fundamental no trivial. Estructura del grupo de Lie abeliano, el grupo circular, topológicamente equivalente a la recta proyectiva real, R P¹. Paralelizable. SO(2) = U(1).

2-esfera

También conocida simplemente como esfera. Estructura compleja; equivalente a la recta proyectiva compleja, C P¹. SO(3)/SO(2).

3-esfera

También conocida como glomo. Paralelizable, U(1)-haz principal sobre la 2-esfera, estructura de grupo de Lie Sp(1), donde también

$\mathrm{S}\mathrm{p}(1)\cong \mathrm{S}\mathrm{O}(4)/\mathrm{S}\mathrm{O}(3)\cong \mathrm{S}\mathrm{U}(2)\cong \mathrm{S}\mathrm{p}\mathrm{i}\mathrm{n}(3)$.

4-esfera

Equivalente a la recta proyectiva cuaterniónica, HP¹. SO(5)/SO(4).

5-esfera

U(1)-haz principal sobre CP². SO(6)/SO(5) = SU(3)/SU(2).

6-esfera

Posee una variedad casi compleja proveniente del conjunto de unidades de octonión puras. SO(7)/SO(6) = G₂/SU (3). La pregunta de si posee un estructura compleja se conoce como el "problema de Hopf", en referencia a Heinz Hopf.

7-esfera

Estructura topológica de cuasigrupo como el conjunto de unidades de los octoniones. Sp(1)-haz principal sobre S⁴. Paralelizable. SO(8)/SO(7) = SU(4)/SU(3) = Sp(2)/Sp(1) = Spin(7)/G₂ = Spin(6)/SU(3). La 7-esfera es de particular interés, ya que fue en esta dimensión en la que se descubrió la primera esfera exótica.

8-esfera

Equivalente a la línea proyectiva octoniónica OP¹.

23-esfera

Es posible un empaquetamiento de esferas altamente denso en un espacio de 24 dimensiones, que está relacionado con las cualidades únicas de la retícula de Leech.

Véase también

Referencias

Bibliografía

• Plantilla:Cite book
• Plantilla:Cite book
• Plantilla:Cite book
• Plantilla:Cite journal
• Plantilla:Cite journal
• Plantilla:Cite journal

Enlaces externos

• Plantilla:MathWorld
• Hypersphere en Planetmath.